granica kubek: oblicz limx→0( ¹_x+ ¹_{x do 2} )= limx→0 (^x−1_{x do 2})

ICSP: te granice są różne. Pierwsza = ∞ Druga = −∞

Jerzy:

	x + 1		1
= limx→0		= [		] = ∞
	x2		0

Jerzy:

	x − 1		−1
limx → 0		− [		] = −∞
	x2		0

kubek: dlaczego − nieskonczonosc skoro −1/0 daje 0

ICSP: Dlaczego 0?

Jerzy: Nie istnieje dzielenie przez 0. Mianownik zmierza do 0 po wartościach dodatnich, czyli ułamek zmierza do minus nieskończoności , bo licznik jest ujemny.

kubek: to moze inaczej wiem ze jak mam np liczba/nieskonczonosc to wtedy mam 0 natomiast w tym przypadku dlaczego jest − nieskonczonosc

Jerzy: Bo licznik jest ujemny, a mianownik stale nieujemny.

kubek: miałem przykłady gdzie granica zmierzala do 3− (po stronie ujemnej) i wychodziło mi np. ⁻²₀₊= to wtedy wychodzi −nieskonczonosc a tutaj nie za bardzo wiem jak to sprawdzic

kubek: aha czyli w tym przypadku nie wazne czy od prawej czy lewej strony 0 mianownik zawsze jest nieujemny wiem jest −nieskonczonosc?

kubek: więc*

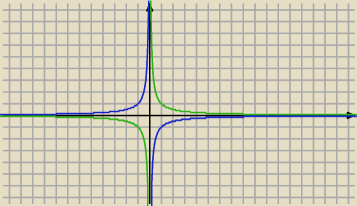
Jerzy: Ad 17:56 zielony: y = 1/x niebieski : y =−1/x w obydwu przypadkach lim = 0

kubek: a co w takiej sytuacji limx→0 ^2x−1_{x do 4 − x do 2}

kubek: wtedy licznik jest ujemny a mianownik zawsze dodatni a rozwiazanie w ksiaze to +nieskończoność

kubek: książce*

ICSP: mianownik jest zawsze dodatni:

	1
Podstawiłem x =		:
	2

1		1		1		1		1 − 4		3
	−		=		−		=		= −
24		22		16		4		16		16

coś chyba nie zawsze ^^ Interesuje Ciebie zachowanie mianownika dla x bliskich 0. Wtedy jest on ujemny.

ICSP: Powinno pomóc rozpisanie: x⁴ − x² = x²(x−1)(x+1)

Jerzy: @ISCP , funkcja g(x) = x⁴ − x² przyjmuje również wartości ujemne. 18:03 , licznik zmierza do − 1 , a mianownik do 0 po wartościach ujemnych,stąd lim = ∞