Geometryczne RubikSon: Przez punkt P należąy do boku trójkąta poprowadzono proste równoległe do dwóch pozostałych boków trójkąta, otrzymują w ten sposób równoległobok. W jakim stosunku punkt P powinien dzieli bok trójkąta, aby pole otrzymanego równoległoboku było największe?

RubikSon: Bump

RubikSon: Ktoś to da radę zrobić?

Chińska podróba 6-latka: ja dam radę , ale z geometrii nie wpisuję rozwiązań bo rysunków nie umiem i nie chcę robić ale w połowie boku musi być ten punkt jeśli odpowiedź cię interesuje

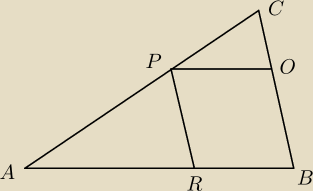Saizou : ΔABC ≡ ΔARP (w skali k) oraz ΔABC ≡ ΔPOC (w skali n). Niech P = P(ABC)

	1		1
P(ARP) =		P oraz P(AOC) =		P.
	k2		n2

1		1
	= 1−
n		k

1		2		1
	= 1 −		+
n2		k		k2

	1		1		1		1
P(RBOP) = P −		P−		P = P(1−		−		) =
	k2		n2		k2		n2

	1		2		1		2		2
P(1−		−1 +		−		) = P(		−		)
	k2		k		k2		k		k2

	2		2
Szukamy największej wartości funkcji f(k) =		−
	k		k2

	1
Podstawmy		= t, wówczas mamy f(t) = 2t−2t2 = g(t)
	k

	−2
Maksimum funkcji t wypada w wierzchołku t =		= {1}{2} i wynosi ono
	2*(−2)

	1		1		1
g(		) =1 1−		=
	2		2		2

1		1
	=		⇒ k = 2 = n
k		2

WNIOSEK: Największe pole RBOP jest wówczas, gdy P leży w połowie boku AC

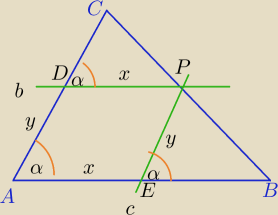Mila: DP||AB i PE||AC P_AEPD=x*y*sinα 1)

	b−y		b
ΔCDP∼ΔABC ⇔		=
	x		c

	(b−y)*c
x=
	b

2)

	(b−y)*c
PAEPD=P(y)=		*y*sinα
	b

	c*sinα
P(y)=		*(by−y2)
	b

Największa wartość w wierzchołku paraboli :

	−b		1
yw=		=		b
	−2		2

	1
y=		b
	2

	1
|CD|=		b
	2

CD		CP
	=1:1 analogicznie		=1:1
DA		PB