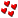rachunek różniczkowy silly goose: Oblicz granicę:

	1		x−2
lim (		−		)
	x2		x3−x

x→0

	4		1
lim (		−		)
	1−x		(x−1)2

x→1

getin:

1		x−2		1		x−2
	−		=		−		=
x2		x3−x		x2		x(x2−1)

	1(x2−1)		x(x−2)
=		−		=
	x2(x2−1)		x2(x2−1)

	x2−1−x2+2x		2x−1
=		=
	x2(x2−1)		x2(x2−1)

	2x−1		2*0−1		−1
limx→0		= limx→0		=		czyli jest to
	x2(x2−1)		02(02−1)		0

	a
wyrażenie typu
	0

	a
pojawienie się wyrażenia typu		sugeruje że możliwe są trzy opcje: granica może wynieść
	0

+∞, −∞ albo w ogóle nie istnieć Aby wiedzieć która z opcji będzie w grze, to trzeba obliczyć granice jednostronne tj. lim_x→0⁺ oraz lim_x→0⁻ Jeśli obie te granice lim_x→0⁺ oraz lim_x→0⁻ będą równe, to wynik granicy lim_x→0 będzie równy wynikowi każdej z granic lim_x→0⁺ oraz lim_x→0⁻ Jeśli obie granice lim_x→0⁺ oraz lim_x→0⁻ nie będą równe, to granica lim_x→0 nie istnieje przy czym 0⁺ traktujesz jako 0,01, zaś 0⁻ jako −0,01

	2x−1		2*0,01−1		−0,98
limx→0+		=		=		=
	x2(x2−1)		0,012*(0,012−1)		0,0001*(−0,9999)

	−0,98
	−0,0001

na górze na minusie, na dole na minusie więc wynik granicy to +∞

	2x−1		2*(−0,01)−1
limx→0−		=		=
	x2(x2−1)		(−0,01)2*((−0,01)2−1)

	−1,02		−1,02
		=		czyli też +∞
	0,0001*(−0,9999)		−0,0001

Ponieważ lim_x→0⁺ oraz lim_x→0⁻ są równe +∞, to lim_x→0 wynosi +∞

4		1		−4		1		−4(x−1)		1
	−		=		−		=		−		=
1−x		(x−1)2		x−1		(x−1)2		(x−1)2		(x−1)2

	−4x+4−1
		=
	(x−1)2

	−4x+3
=
	(x−1)2

	−4x+3		−4*1+3		−1
limx→1		=		=
	(x−1)2		(1−1)2		0

	−4x+3		−4*1,01+3		−4,04+3
limx→1+		=		=		=
	(x−1)2		(1,01−1)2		(0,01)2

	−1,04
		= −∞
	0,0001

	−4x+3		−4*0,99+3		−3,97+3
limx→1−		=		=		=
	(x−1)2		(0,99−1)2		(−0,01)2

	−0,97
		= −∞
	0,0001

Ponieważ granice lim_x→1⁺ oraz lim_x→1⁻ są równe i wynoszą −∞, to

	−4x+3
limx→1		= −∞
	(x−1)2

silly goose: Dziękuje baardzo