Oblicz pole obszaru ograniczonego wykresami funkcji
Jarek: Oblicz pole obszaru ograniczonego wykresami funkcji
f(x)=|2x+2|−1 oraz g(x)=|x−2|+3
29 mar 20:12
Mila:
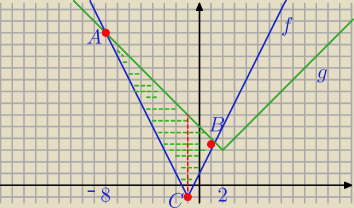
f(x)=|2x+2|−1
g(x)=|x−2|+3
Punkty wspólne:
1)
x<−1
f(x)=−2x−2−1 i g(x)=−x+2+3
−2x−3=−x+5
−x=8, x=−8 i y=13
A=(−8,13)
2) x≥1 i x<2
f(x)=2x+2 −1 i g(x)=−x+5
2x+1=−x+5
3x=4
Licz pole
29 mar 22:10
Jarek: a co z C?
29 mar 22:21
chichi:
f(x)=2|x+1|−1 ⇒ C=(−1, −1)
29 mar 22:30
Mila:
f(−1)=0−1=−1
C=(−1,−1)
Za pomocą całki, czy szkolnym sposobem masz obliczyć pole?
29 mar 22:32
Jarek: szkolnym
29 mar 22:34
Mila:
Jak liczyliście w szkole, co pamiętasz?
29 mar 22:47
Jarek: P=1/2 ah
29 mar 22:52
Jarek: i p=a*h/2 najbardziej
29 mar 22:53
Mila:
A wektory i wyznacznik były?
29 mar 22:54
Jarek: nie, raczej nie
29 mar 22:55
Jarek: to jest zadanie z 1 klasy tech
29 mar 22:58
Mila:
1) Oblicz długość boku AC.
2) Oblicz odległość punktu B od prostej y=−2x−3
I podaj obliczone wyniki.
29 mar 22:59
chichi:
Ten wzór jest w tablicach, nie musiał pojawiać się na lekcji

29 mar 23:04
Jarek:
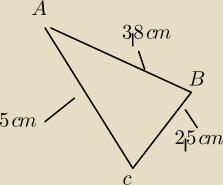
cos takiego?
29 mar 23:14
Jarek: h= 2cm
29 mar 23:16
29 mar 23:17
Jarek: P=1/2(−8,13)*(1,4)*(−1,−1)
29 mar 23:28
chichi:
Co Ty punkty sobie mnożysz?

29 mar 23:31
Jarek: dobra, mam tyle ile mam, dzieki za pomoc, sproboje poogladac jakies poradniki bo chyba tak
bedzie najlepiej
29 mar 23:35
Mila:
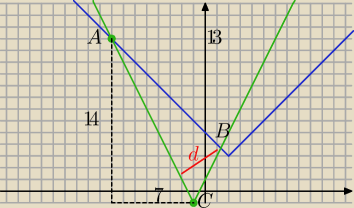
Jarek tak nie można.
A=(−8,13), C=(−1,−1)
Liczysz długość |AC| z twierdzenia Pitagorasa z rysunku:
|AC|
2=7
2+14
2}=49+196=245=5*49
|AC|=
√5*49=7
√5
Albo z wzoru na długość odcinka; Na pewno masz w podręczniku.
A=(x
1,y
1), B=(x
2,y
2)
|AB|=
√(x2−x1)2+(y2−y1)2
===================
|AC|=
√(−1−(−8))2+(−1−13)2=
√72+(−14)2=
√245
2)
| | 4 | | 11 | |
Odległość punktu B=( |
| , |
| ) od prostej AC: y=−2x−3 |
| | 3 | | 3 | |
2x+y+3=0
Wzór :
| | 1 | | 28 | | 7*14 | |
PΔ= |
| *7√5* |
| = |
| |
| | 2 | | 3√5 | | 3 | |
29 mar 23:52
Mila:
II sposób
AC
→=[7,−14]
| | 4 | | 11 | | 28 | | 28 | |
AB→=[ |
| −(−8), |
| −13}]=[ |
| ,− |
| ] |
| | 3 | | 3 | | 3 | | 3 | |
| | 1 | | 28 | | 28 | |
PΔ= |
| *|7*(− |
| )−(−14* |
| )|= |
| | 2 | | 3 | | 3 | |
29 mar 23:52
chichi:
III sposób
| | 28√2 | | 7√5 | | 14√2+14√5 | |
|AB|= |
| , |AC|=7√5, |BC|= |
| , p= |
| |
| | 3 | | 3 | | 3 | |
| | 14√2+14√5 | | 14√2+14√5 | | 28√2 | | 14√2+14√5 | |
P=√ |
| ( |
| − |
| )( |
| −7√5) |
| | 3 | | 3 | | 3 | | 3 | |
| | 14√2+14√5 | | 7√5 | | 98 | |
( |
| − |
| )= |
| [ j2] |
| | 3 | | 3 | | 3 | |
Ale raczej nie polecam tej drogi

30 mar 00:06
blabla:
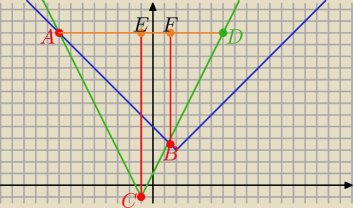
| | 4 | | 11 | |
A(−8,13), C(−1,−1), D(6,13) , B( |
| , |
| ) |
| | 3 | | 3 | |
P(ABC)= P(ADC)=P(ABD)
| | 11 | | 28 | |
|AD|=14 , |CE|=14 , |BF|= 13− |
| = |
| |
| | 3 | | 3 | |
| | 1 | | 1 | | 28 | |
P(ABC)= |
| *14*14 − |
| *14* |
| |
| | 2 | | 2 | | 3 | |
============
30 mar 00:30
chichi:
Chyba się ' = ' wkradł zamiast ' − '

30 mar 00:33
blabla:
Oczywiście miało być :
P(ABC)=P(ADC)−P(ABD)
30 mar 00:34
blabla:
No i po ptokach


30 mar 00:41
chichi:
Można też ten trójkąt zamknąć w prostokącie i od jego pola odjąć 3 pola trójkątów
prostokątnych, nieco więcej pracy. Ile ludzi tyle pomysłów +1

30 mar 00:44
Qulka: To zadanie z 1 klasy ze str 186 i jedynie znają Twierdzenie Picka które było na str 69
30 mar 09:39
Chińska podróba 6-latka: jaki to podręcznik?
30 mar 10:13
Qulka: Babiański
30 mar 11:21
Chińska podróba 6-latka: Nowa Era? podstawa czy rozszerzenie?
30 mar 11:24
Qulka: nowa era jednoczesnie podstawa i rozszerzenie ( taka zółta)
30 mar 11:52
Saizou :
Qulka B nie jest punktem kratowym, wzór Picka nie zadziała.
30 mar 12:21
Chińska podróba 6-latka:
żółtą to ja nazywam rozszerzeniem , podstawa jest niebieska

30 mar 12:32
uou:

30 mar 12:32
Chińska podróba 6-latka:

30 mar 12:38
Qulka: no tak w zadaniu mam f(x)=|2x+2|−1 oraz g(x)=|x−2|+
1 
30 mar 16:01
 f(x)=|2x+2|−1
g(x)=|x−2|+3
Punkty wspólne:
1)
x<−1
f(x)=−2x−2−1 i g(x)=−x+2+3
−2x−3=−x+5
−x=8, x=−8 i y=13
A=(−8,13)
2) x≥1 i x<2
f(x)=2x+2 −1 i g(x)=−x+5
2x+1=−x+5
3x=4
f(x)=|2x+2|−1
g(x)=|x−2|+3
Punkty wspólne:
1)
x<−1
f(x)=−2x−2−1 i g(x)=−x+2+3
−2x−3=−x+5
−x=8, x=−8 i y=13
A=(−8,13)
2) x≥1 i x<2
f(x)=2x+2 −1 i g(x)=−x+5
2x+1=−x+5
3x=4

 cos takiego?
cos takiego?

 Jarek tak nie można.
A=(−8,13), C=(−1,−1)
Liczysz długość |AC| z twierdzenia Pitagorasa z rysunku:
|AC|2=72+142}=49+196=245=5*49
|AC|=√5*49=7√5
Albo z wzoru na długość odcinka; Na pewno masz w podręczniku.
A=(x1,y1), B=(x2,y2)
|AB|=√(x2−x1)2+(y2−y1)2
===================
|AC|=√(−1−(−8))2+(−1−13)2=√72+(−14)2=√245
2)
Jarek tak nie można.
A=(−8,13), C=(−1,−1)
Liczysz długość |AC| z twierdzenia Pitagorasa z rysunku:
|AC|2=72+142}=49+196=245=5*49
|AC|=√5*49=7√5
Albo z wzoru na długość odcinka; Na pewno masz w podręczniku.
A=(x1,y1), B=(x2,y2)
|AB|=√(x2−x1)2+(y2−y1)2
===================
|AC|=√(−1−(−8))2+(−1−13)2=√72+(−14)2=√245
2)









