Prawdopodobieństwo zmartwionyuczeń: Cześć, jak w zadaniach typowo maturalnych wyznaczyć sumę prawdopodobieństwa? Zawsze mam z tym problem. Głównie używa się tego przy wzorze na prawdopodobieństwo warunkowe. P(A|B) = ^P(A∩B)_P(B) i problem pojawia się u mnie przy P(A∩B). Przykładowe zadanie (ale prosiłbym o sposób myślenia, a nie rozwiązanie): Wśród 10 tysięcy mieszkańców pewnego miasta przeprowadzono sondaż dotyczący budowy przedszkola publicznego. Wyniki sondażu przedstawiono w tabeli. Badane grupy Liczba osób popierających budowę przedszkola Liczba osób niepopierających budowy przedszkola Kobiety 5140 1860 Mężczyźni 2260 740 Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, popiera budowę przedszkola, jeśli wiadomo, że jest mężczyzną.

zmartwionyuczeń: A − popiera budowę B − jest mężczyzną P(B) = ³⁰⁰⁰₁₀₀₀₀ = ³₁₀ P(A∩B) =

Qulka: no to AnB to męzczyżni którzy popierają czyli 2260

zmartwionyuczeń: https://zadania.info/d466/6236295 Tutaj to zadanie w nieco przyjemniejszej formie, łatwiej będzie odczytać.

Qulka: więc P(AnB) = 0,226

Qulka: https://matematykaszkolna.pl/strona/4649.html

zmartwionyuczeń: No dobrze, a w tym zadaniu: W sklepie "Masz szczęście" można kupić gumki produkowane przez firmę A i firmę B. 40% wszystkich gumek pochodzi z firmy A, a reszta a firmy B. Wiemy, że 1% gumek wyprodukowanych w firmie A jest wadliwe, a wsód gumek firmy B, gumki wadliwe to 2%. Klient wszedł do sklepu, kupił jedną gumkę i okazało się, że miał szczęście i gumka okazała się nie mieć wady. Jakie jest prawdopodobieństwo, że wyprodukował ją zakład A? F − gumka nie ma wady E − gumka pochodzi z firmy A P(E|F) = ... Po rozrysowaniu drzewka P(EnF) to będzie tylko "gałąź", w której gumka nie ma wady i jest wyprodukowana przez firmę A?

F&M: To jest prawdopodobieństwo całkowite / wzór Bayesa

Qulka: tak to będzie tylko ta jedna gałąź

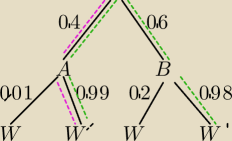
Mila: W− wadliwa W' − bez wady

	0.4*0.99
P(A/W')=		≈0.4024
	0.4*0.99+0.6*0.98