Planimetria, trójkąt myszojeleń: W trójkącie równoramiennym ABC podstawa ma długość x, a kąt przy wierzchołku C ma miarę 120°. Na bokach AB, BC i CA wybrano punkty odpowiednio K, L, M tak, że |AK| = 3|KB|, |BL| = 2|LC|, |CM| = 4|MA|. Oblicz długości boków trójkąta KLM i jego pole.

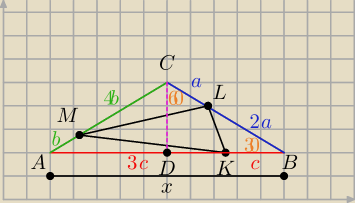
Saizou : Masz podpowiedź w postaci rysunku

Mila: Twierdzenie Routha

	2*4*3+1
PΔKLM=		*PΔABC
	(2+1)*(4+1)*(3+1)

	5
PΔKLM=		PΔABC
	12

mam pytanie: na podstawie rysunku Saizou: KB=x/4 LB=2x√3/9 (wyliczamy z trojkata CBD ekierki) ∡KBL=30 z tw. cosinusów KL=..... AK=3x/4 AM=x√3/12 ∡MAK=30^o z tw. cosinusow dla ΔAKM MK=.... CL=x√3/9 CM=x√3/4 ∡MCL=120 z tw. cosinusów dla ΔMCL ML=....

Mila: 3a=5b

	3		3		x√3		x√3
b=		a=		*		=		, popraw CM i AM.
	5		5		9		15

Coś jeszcze?