dowód Mateusz: W okrąg wpisano czworokąt wypukły KLMN Bok KL jest średnicą tego okręgu, a przekątne KM i LN przecinają się w punkcie P, zaś styczne w punktach M i N przecinają się w punkcie Q Wykaż,że trójkąt PMQ jest równoramienny

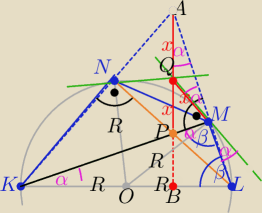
ϱki: Trzy wysokości w ΔAKL przecinają się w punkcie P ( ortocentrum) ΔABL i KLM są podobne z cechy (kkk) to ∡MKL=∡BAL=α= ∡KMO=∡QMA ΔAPM prostokątny , okrąg opisany na nim ma średnicę |AP|=2x to |PQ|=|QM|=x i mamy tezę ΔPMQ −−− równoramienny