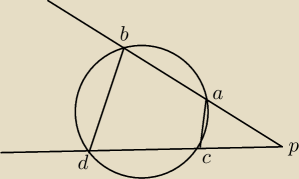Dany jest okrąg który przecięto dwoma półprostymi k i l wychodzącymi z punktu P Grzesiek: Dany jest okrąg który przecięto dwoma półprostymi K i L wychodzącymi z punktu P. Prosta K przecina okrąg w punktach A i B a prosta L w punktach C i D.

	|CP| * |DP|
Wykaż że |AP| =
	|BP|

chichi:

	|DP|*|CP|
Wprost z tw. o odcinkach siecznych: |DP|*|CP|=|BP|*|AP| ⇒ |AP|=		Q.E.D.
	|BP|

Grzesiek: Dzięki