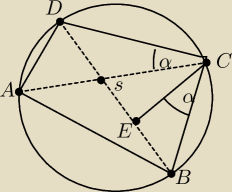
dowodzenie karola44: Przekątne czworokąta ABCD wpisanego w okrąg przecinają się w punkcie S , a punkt E jest takim punktem przekątnej BD , że |∡DCS | = |∡BCE | (zobacz rysunek).

	|CD|*|CB |
Wykaż, że |CE|=
	|CA|

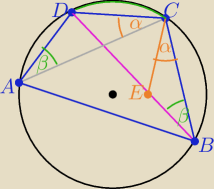a@b: 1/ kąty β wpisne oparte na łuku DC mają równe miary 2/ trójkąty ACD i BCE są podobne z cechy (kkk) to:

	|CD|		|CA|		|CD|*|CB|
		=		⇒ |CE|=
	|CE|		|CB|		|CA|

c. n.w