 Zadanko dla chętnych
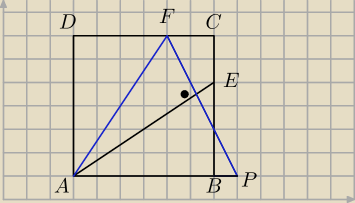
Punkty E i F leżą odpowiednio na bokach BC i CD kwadratu ABCD, przy czym EC=FC.
Prosta przechodząca przez punkt F i prostopadła do prostej AE przecina prostą AB w punkcie P.
Wykaż, że AF=PF.
Zadanko dla chętnych
Punkty E i F leżą odpowiednio na bokach BC i CD kwadratu ABCD, przy czym EC=FC.
Prosta przechodząca przez punkt F i prostopadła do prostej AE przecina prostą AB w punkcie P.
Wykaż, że AF=PF.
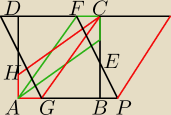 |AF|=|AE| , bo ΔAFD ≡ ΔABE
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
|PF|=|GC|
|GC|=|HC| bo ΔGBC ≡ ΔHDC
|HC|=|AE| zatem |AF|=|PF|
c.k.d
|AF|=|AE| , bo ΔAFD ≡ ΔABE
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
|PF|=|GC|
|GC|=|HC| bo ΔGBC ≡ ΔHDC
|HC|=|AE| zatem |AF|=|PF|
c.k.d