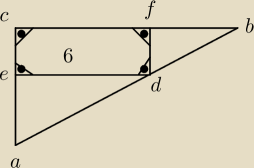
 Może ktoś umiałby mi pomóc? Na przyprostokątnych AC i BC trójkąta prostokątnego ABC leżą
wierzchołki − odpowiednio E i F prostokąta CEDF. Wierzchołek D tego prostokąta leży na
przeciwprostokątnej AB tak, że |AD| : |DB| = 2 : 1. Pole prostokąta CEDF jest równe 6.
Pole trójkąta ABC jest równe?
A. 13
B. 11
C. 10
D. 12
Może ktoś umiałby mi pomóc? Na przyprostokątnych AC i BC trójkąta prostokątnego ABC leżą
wierzchołki − odpowiednio E i F prostokąta CEDF. Wierzchołek D tego prostokąta leży na
przeciwprostokątnej AB tak, że |AD| : |DB| = 2 : 1. Pole prostokąta CEDF jest równe 6.
Pole trójkąta ABC jest równe?
A. 13
B. 11
C. 10
D. 12
| 1 | 1 | |||
ΔBFD∼ΔBCD w skali k= | ⇔PΔBFD= | P | ||
| 3 | 9 |
| 2 | 4 | |||
ΔBCD∼ΔBCD w skali k1= | ⇔PΔBCD= | P | ||
| 3 | 9 |
| 1 | 4 | ||
P+6+ | P=P | ||
| 9 | 9 |
| 4 | |
P=6 | |
| 9 |
| 9 | 27 | |||
P=6* | = | |||
| 4 | 2 |
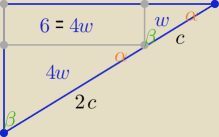 P(ABC)= 9w P▭=4w=6 ⇒ w=1,5
P(ABC)=9*1,5= 13,5
=================
P(ABC)= 9w P▭=4w=6 ⇒ w=1,5
P(ABC)=9*1,5= 13,5
=================