zadanie z geometrii maturalnyy: dzien dobry dostalem takie zadanie z geometrii od nauczycielki i nie moge sobie z nim poradzic. Przekatne czworokata ABCD wpisanego w okrag o promieniu R przecinaja sie w punkcie S. Wiedzac ze AB=BC=a oraz BD=m, znajdz promien okregu opisanego na trojkacie BCS.

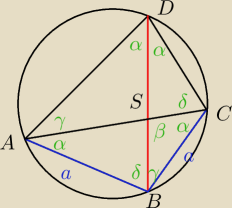
Saizou : γ = 180−α−β δ = β−α Niech r będzie promieniem okręgu opisanego na BCS. Z tw. sinusów

a
	= 2r
sinβ

∡A = γ+α = 180−α−β+α = 180−β

m		m		m
	=2R →		= 2R →sinβ =
sin(180−β)		sinβ		2R

a		aR
	=2r →r =
m   2R		m