Oblicz całkę KrystianoC: Cześć, mam do rozwiązania taki przykład: ∫||x|−2|dx, przy granicach całki (−4,4). Wiem, że wynik wyniesie 8 ale nie umiem tego policzyć. Rozłożyłam to na przypadki: 1) x ∊(−2,2) 2) x ∊(−∞,−2) 3) x ∊(2,+∞) ale nie wiem czy są poprawne i jak to dalej uwzględnić. Bardzo proszę o pomoc

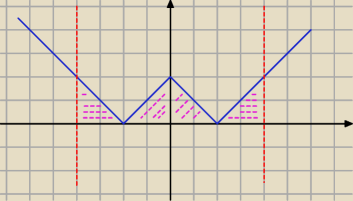
Maciess: Najszybciej to narysowac wykresik tej funkcji i policzyc pole To wyjdą jakies trójkąciki pewnie. Jak chcesz rozbijac na przypadki to rozbijasz na sume całek. Dobrze jest też widzieć, że funkcja podcalkowa jest parzysta (a przedział całkowania symetryczny). Mozesz zamienic to na 2*calka na (0,4) i zawsze mniej liczenia.

KrystianoC: Teraz to już kompletnie nie czaję Skoro łatwiej to pewnie jest tak jak mówisz ale w dalszym ciągu nie wiem jak się za to zabrać i co policzyć

Maciess:

KrystianoC: Okej, czyli to będą jakieś 4 przedziały jednak więc coś pominąłem A jak dalej policzyć te pola?

Maciess: Policzenie pól trójkątów zostawiam tobie Jak bardzo chcesz to można te całke (dla przedzialu (0,4) ) rozbic na (od 0 do 2)∫−(x−2) dx + (od 2 do 4) ∫x−2 dx