algebra liniowa salamandra: 13. Napisz równanie parametryczne prostej prostopadłej do płaszczyzny 2x − 3y + z = 5 i przechodzącej przez punkt (0, 0, 5). 14. Napisz ogólne równanie parametryczne prostej zawartej w płaszczyźnie 2x − 3y + z = 5 i przechodzącej przez punkt (0, 0, 5). Nie chcę rozwiązania na razie rozwiązania, bo 13 mam, ale mam pytanie, czy jest coś podchwytliwego w 14−tym, że jest napisane OGÓLNE równanie....?

ABC: wstyd przynosisz naszemu miastu takimi pytaniami w 13 masz dokładnie jedną taką prostą a w 14 cały pęk prostych leżących w tej płaszczyźnie

salamandra: wybacz, tak to jest, gdy ćwiczenia wyprzedzają wykłady wszystko robię na razie intuicyjnie. W takim razie przedstawię rozwiązanie 13−tego i prosiłbym o wskazówkę do 14−tego, bo nie wiem w takim razie, o co tam chodzi. 13. P=(0,0,5) v=(2,−3,1) Jako, że wektor normalny jest prostopadły do tej płaszczyzny, to równanie tej prostej to: x=2t y=−3t z=5+t

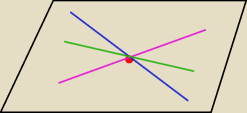
ABC: to jest do 14

Jerzy: Nie ma pojęcia „ogólne równanie parametryczne prostej”