 V = 3m3
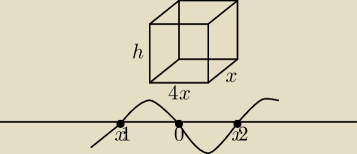
Wiemy, że jeżeli jedna z krawędzi podstawy ma długość x, a druga jest od niej cztery razy
dłuższa, więc ta druga krawędź będzie wynosiła 4x.
Wysokość graniastosłupa to h (jak na rysunku). h można policzyć ze wzoru V/Pp = 3m3/4x2
Chcemy by pojemnik wykonany z graniastosłupa o długościach x, 4x, h (co równe jest x, 4x,
3m3/4x2), którego objętość jest równa 3m3, miał jak najniższy koszt.
Do obliczenia ceny pojemnika trzeba znać pole boczne (Pb) i dwa pola podstawy (Pp)
2 * Pp * 60zł/m2 = 2 * 4x m * x m * 60zł/m2 = 480x2 zł
Pb = (2 * 4x m * h m + 2 * x m* h m) * 40zł/m2 = (10x * h) *40zł = 10x * 3/4x2 *40zł = 300/x
zł
P(x) = 480x2 + 300/x zł
x>0
Liczymy pochodną P'(x) = 960x − 300/x
960x − 300/x > 0 /*x2 :10
96x3 − 30x > 0 / :3
32x3 − 10x > 0
32x * (x2 − 10/32) > 0
32x (x + √5/4)(x − √5/4) > 0
x=0 x= −√5/4 x = √5/4
Rysujemy wykres, co ważne najwyższa potęga jest dodatnia: (nie wiedziałem jak w rysunku
wprowadzić liczby i wprowadziłem x1 dla −√5/4 i x2 dla √5/4.
Pochodna P'(x) jest niższa od zera dla przedziału x∊(0;√5/4), czyli funkcja P(x) maleje w
przedziale x∊(0;√5/4)
W takim razie Pmin dla x = √5/4, wtedy cena pojemnika będzie najniższa.
x = √5/4 h = 3/[4(√5/4)2] = 3 / 20 * 16 = 12/5
Odp./ x = √5/4 h = 12/5
V = 3m3
Wiemy, że jeżeli jedna z krawędzi podstawy ma długość x, a druga jest od niej cztery razy
dłuższa, więc ta druga krawędź będzie wynosiła 4x.
Wysokość graniastosłupa to h (jak na rysunku). h można policzyć ze wzoru V/Pp = 3m3/4x2
Chcemy by pojemnik wykonany z graniastosłupa o długościach x, 4x, h (co równe jest x, 4x,
3m3/4x2), którego objętość jest równa 3m3, miał jak najniższy koszt.
Do obliczenia ceny pojemnika trzeba znać pole boczne (Pb) i dwa pola podstawy (Pp)
2 * Pp * 60zł/m2 = 2 * 4x m * x m * 60zł/m2 = 480x2 zł
Pb = (2 * 4x m * h m + 2 * x m* h m) * 40zł/m2 = (10x * h) *40zł = 10x * 3/4x2 *40zł = 300/x
zł
P(x) = 480x2 + 300/x zł
x>0
Liczymy pochodną P'(x) = 960x − 300/x
960x − 300/x > 0 /*x2 :10
96x3 − 30x > 0 / :3
32x3 − 10x > 0
32x * (x2 − 10/32) > 0
32x (x + √5/4)(x − √5/4) > 0
x=0 x= −√5/4 x = √5/4
Rysujemy wykres, co ważne najwyższa potęga jest dodatnia: (nie wiedziałem jak w rysunku
wprowadzić liczby i wprowadziłem x1 dla −√5/4 i x2 dla √5/4.
Pochodna P'(x) jest niższa od zera dla przedziału x∊(0;√5/4), czyli funkcja P(x) maleje w
przedziale x∊(0;√5/4)
W takim razie Pmin dla x = √5/4, wtedy cena pojemnika będzie najniższa.
x = √5/4 h = 3/[4(√5/4)2] = 3 / 20 * 16 = 12/5
Odp./ x = √5/4 h = 12/5
 W poprzednim rozwiązaniu źle policzona została pochodna i dalej też już jest źle.
Powinno być.
W poprzednim rozwiązaniu źle policzona została pochodna i dalej też już jest źle.
Powinno być.
| 300 | 960x3 − 300 | |||
Liczymy pochodną P'(x) = 960x − | = | |||
| x2 | x2 |
| 300 | 10 | 5 | ||||
x3 = | = | = | ||||
| 960 | 32 | 16 |
| 960x3 − 300 | ||
Rysujemy przybliżony wykres pochodnej P'(x) = | ||
| x2 |