Geometria analityczna Dżul: W trójkącie równoramiennym ABC o ramionach AC I BC dane są A=(−3,−4) i B=(5,2). Wysokość trojkata poprowadzona do podstawy AB ma długość 10. Oblicz współrzędne punktu C rozpatrz wszystkie przypadki.

chichi: C=(−5, 7) ∨ C=(7, 9)

chichi: Zjadłem minus przy 9, oczywiście C=(7, −9)

Dżul: A czy mógłby to ktoś rozrysować i wytłumaczyć? Ja to narysowałam W układzie współrzędnych wyznaczyłam równanie AB i jej środek i coś mi nie wyszło jak liczyłam odległość punktu od prostej.

chichi: Najpierw trzeba wyznaczyć równanie prostej prostopadłej przechodzącej przez środek, na której leżą wierzchołki C i z odległości punktu od prostej, lub zaczepić w środku odcinka AB okrąg o promieniu długości 10 i znaleźć jego punkty przecięcia właśnie z tą prostą

ICSP: Podaj 1^o równanie prostej AB 2^o współrzędne środka odcinka AB 3^o równanie prostej prostopadłej do AB 4^o współrzędne pkt C 5^o równanie powstałe z zastosowania wzoru na odległość punktu od prostej

chichi:

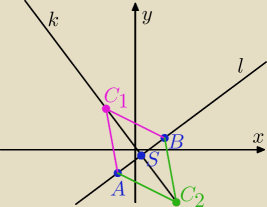
	4		1		3		7
k: y=−		x+		l: y=		x−
	3		3		4		4

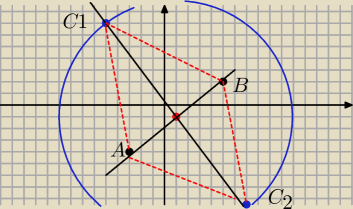
6latek: A=(−3,−4) B=(5,2) Wspolczynnik kierunkowy m prostej AB

	6		3
m=		=
	8		4

Wspolrzedne srodka S odcinka AB x_s=1 i y_s=−1 S=(1,−1) (obliczenia wykonuje sie w pamieci Rownanie prostej prostopadlej do AB i przechodzacej przez punkt S

	4
m1=−		i S=(1,−1)
	3

y=m₁(x−x₀)+y₀

	4
y=−		(x−1)−1
	3

	4		1
y=−		x+
	3		3

Punkty wierzcholka C beda to punkty przeciecia okregu o rownaniu (x−1)²+(y+1)²=100 i prostej

	4		1
z prosta y=−		x+
	3		3

	4		4
(x−1)2+(−		x+		)2=100
	3		3

	16		32		16
x2−2x+1+		x2−		x+		=100
	9		9		9

25		50		25
	x2−		x+		=100 /*9
9		9		9

25x²−50x+25=900 25x²−50x−875=0 Δ=90000 √Δ=300

	50−300
x1=		=−5
	50

	50+300
x2=		=7
	50

	4		1
jesli x=−5 to y=−		*(−5)+		=7 C1=(−5,7)
	3		3

	4		1
jesli x=7 to y=−		*7+		=−9 C2=(7,−9)
	3		3