Aksjomat zadanie 12 Dżul: Dany jest trójkąt prostokątny ABC, w którym kąt C jest prosty. |CA|=2√2 i |CB|=2 . Wykaż że środkowe BD i CE tego trójkąta są do siebie prostopadłe

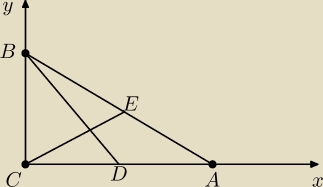
getin: Niech C = (0,0), A = (2√2,0), B = (0, 2). Wówczas D − środek odcinka AC, więc D = (√2,0) E − środek odcinka AB, więc E = (√2,1) Korzystamy ze wzoru na współczynnik kierunkowy prostej

	y2−y1
a =
	x2−x1

	yE−yC
aCE =
	xE−xC

	1−0		1
aCE =		=
	√2−0		√2

	yD−yB
aBD =
	xD−xB

	0−2		−2
aBD =		=
	√2−0		√2

Aby pokazać że środkowe BD i CE są prostopadłe, wystarczy pokazać że a_CE*a_BD = −1

	1		−2		−2
aCE * aBD =		* (		) =		= −1
	√2		√2		2

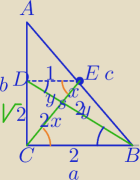Mila: 1) c=2√3 |CE|=√3 |DB|=√6

	1
2) ΔDES∼ΔBCS w skali k=
	2

	√3
x=
	3

	√6
y=
	3

3) Tw. odwrotne do tw. PItagorasa

	√3		√6
12= ? (		)2+(		)2
	3		3

	3		6
1=		+		− równość prawdziwa
	9		9

CE⊥BD

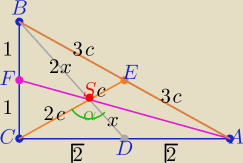Eta: Trzy środkowe dzielą trójkąt na 6 trójkątów o równych polach

	1		√2
to P(CDS)=		*2√2 =
	6		3

P(CDS)= cx*sinα

	√2
sinα=		6c=2√3 ⇒ 3c= √3 i 3x=√6/3=√2*√3/3
	3cx

	√2
sinα=		=1
	√3*√2*√3/3

α=90^o zatem środkowe BD i CE są prostopadłe c.n.w.

chichi: I to jest właśnie piękno geometrii, brawo

Eta:

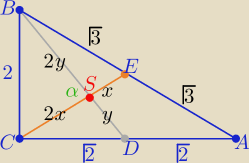
	√3
|AB|=√8+4=2√3 |CE|=3x=√3 ⇒ x=
	3

	√2*√3
|BD|=√2+4=√6=√2*√3= 3y ⇒ y=
	3

z tw. odwrotnego do tw. Pitagorasa w ΔCBS 4y²+4x²= 4 x²+y²=1

	1		2
		+		= 1
	3		3

zatem α= 90^o ⇒ BD⊥CE

Eta: Ooo ... Mila już podała