Pole trójkąta BoosterXS:

	12
W trójkącie ABC bok BC ma miarę 15, sin kąta przy wierzchołku A wynosi		oraz sinusa
	13

	4
kąta przy wierzchołku B wynosi
	5

Oblicz pole trójkąta ABC. Z twierdzenia sinusów obliczyłem bok AC, wynosi 13. Następnie z jedynki trygonometrycznej obliczyłem cosinus kąta przy wierzchołku B. I tu zaczynają się problemy, bo nie wiem czy mam wziąć cosinusa ujemnego dla kąta rozwartego czy dodatniego dla kąta ostrego.

	3
Przyjmując cos=		i korzystając z twierdzenia cosinusów wychodzi, że trzeci bok (AB) ma
	5

długość 4 lub 14. Czy w takim razie pole trójkąta mam rozważyć na dwa przypadki, czy któraś z odpowiedzi nie pasuje?

getin: naprzeciwko dłuższego boku leży większy kąt Zatem kąt przy wierzchołku A jest większy niż ten przy wierzchołku B Czyli ten który jest przy wierzchołku B musi być ostry

	4
sin(B) =		więc kąt B = 53o
	5

	12
sin(A) =		więc kąt A = 67o lub 113o
	13

Przyjmując że oba kąty przy A i B będą ostre, to ten przy wierzchołku C też wyjdzie ostry 180^o − 53^o − 67^o = 60^o

	3
więc bierzesz dodatniego cosinusa czyli		na plusie
	5

i faktycznie, będą dwa przypadki pola trójkąta (dla |AB|=4 oraz dla |AB|=14), obie pasują

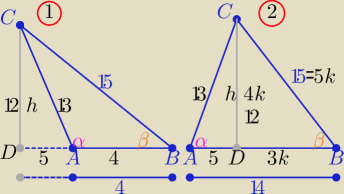
Eta: Jeżeli sinα>0 to α−−ostry lub rozwarty β nie może być rozwarty , bo naprzeciwko β bok 13 < 15 stąd mamy dwa przypadki 1/ PΔ= 24 2/ PΔ= 84

BoosterXS: Bardzo dziękuję za pomoc. Zadanie jest ze zbioru zadań Pazdro 2 klasa (poziom podstawowy) dla osób po szkole podstawowej, numer 7.49 W odpowiedziach podają tylko jedno rozwiązanie P=84 j². Czy jest sens zgłosić to do wydawnictwa, aby poprawili w kolejnych wersjach zbioru?

getin: Wydaje mi się że warto zgłosić. Niestety początkowe wersje książek potrafią mieć sporo błędów