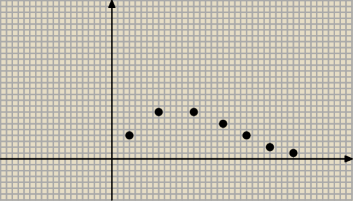
Monotoniczność i ograniczenie ciągu gofruj: Mam pytanie o monotoniczność i ograniczenia ciągu który wygląda jak na załączonym rysunku. Czy jak podać monotoniczność, to poprawne jest stwierdzenie, że do n = 3 wyrazu ciąg jest "niemalejący", oraz malejący od n = 4? Czy jak mam podać ograniczenia, to można stwierdzić, że jest − ograniczony z góry wartością a₃ − ograniczony z dołu zerem (jeśli faktycznie dąży do zera)?

Jerzy: Czy to jest ciąg 7 − mio wyrazowy ?

gofruj: nie, może za bardzo uprościłem, jest normalnie wzorek podany i się ciągnie w nieskończoność.

an+1
	wychodzi mi
an

a) ≥ 1 dla n ≤ 3, b) < 1 n > 4 stąd ten wykresik

ICSP: 1^o tak (z uwagą, że jest malejący dla n ≥ 3) 2^o tak (ograniczony z góry przez a₃ lub tez przez a₂ ) 3^o tak, zerem lub dowolną liczbą ujemną (zakładając, że ma tylko dodatnie wyrazy)

gofruj: Dziękuję bardzo, dopytam się jeszcze − jak są wyrazy tylko dodatnie, a jest pytanie "ogólne" o ograniczoność, to mówię, że jest ograniczony A = a₃ (lub a₂)? Definicję suchego terminu "ograniczoność" wziąłem np. stąd (patrząc na definicję z modułem) (https://epodreczniki.open.agh.edu.pl/openagh-podreczniki_view.php?mode=view&categId=4&handbookId=58&moduleId=380)

ICSP: albo pytasz o ograniczoność albo nie (nie ma czegoś takiego jak pytanie ogólne o ograniczoność) To, że wyrazy są dodatnie nie oznacza, że ciąg jest ograniczony. W tym przypadku tak jest, ale w ogólnym nie musi tak być. Najlepiej połączyć tą informację z monotonicznością ciągu( musi być malejący przynajmniej od pewnego miejsca). Wtedy wiesz na pewno, że jest ograniczony.