równoległobok goosia: Na boku AB równoległoboku ABCD wybrano punkt E tak,że <ADE=<BDC=β Okrąg o środku w punkcie S przechodzący przez punkty E i B jest styczny do boku BC w punkcie B Wykaż,że AS=CS

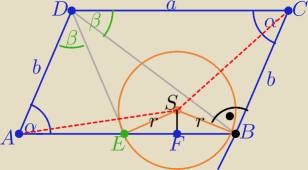
Eta: 1/ trójkąty AED i BDC są podobne z cechy ( kkk)

	b		|AE|		b2
to		=		⇒ |AE|=
	a		b		a

	b2		a2−b2
to |EB|= a −		=
	a		a

	1		a2−b2
i |FB|=|EF|=		|EB|=
	2		2a

2/ z tw, Pitagorasa w ΔBCS : |SC|²=r²+b² w ΔAFS : |AS|²= |AF|²+|SF|²

	b2		a2−b2		a2+b2		a2−b2
|AF|=		+		=		i |SF|=r2−
	a		2a		2a		2a

	a2+b2		a2−b2
to |AS|2 = (		)2−(		)2+r2
	2a		2a

	4a2b2
|AS|2=		+r2
	4a2

|AS|² = b²+r²=|SC|² i mamy tezę: |AS|=|CS| ===========