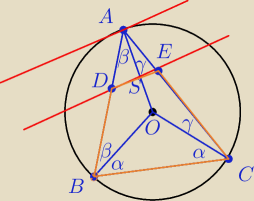
Okrąg, trójkąt, dowód Szkolniak: Treść: W okrąg o(O,R) wpisano trójkąt ABC. Przez wierzchołek A poprowadzono styczną do okręgu, a następnie poprowadzono równoległą do tej stycznej przecinającą boki AB i AC odpowiednio w punktach D i E. Wykaż, że na czworokącie BCDE można opisać okrąg. |OB|=|OC|=|OA|=R, zatem trójkąty ABO, ACO, BCO są równoramienne, co zaznaczyłem poprzez kąty na rysunku. Wiemy, że kąty ''dookoła'' punktu S są równe 90^o. Z kątów BOA, AOC, BOC otrzymujemy, że : 180^o−2α+180^o−2β+180^o−2γ=360 90^o−α+90^o−β+90^o−γ=180^o α+β+γ=90^o Niech kąt BDS ma miarę x, a kąt CES ma miarę y. Z czworokątów BOSD oraz CESO otrzymujemy, że x=β+90^o i y=γ+90^o I teraz musimy pokazać, że: α+γ+x=180^o oraz α+β+y=180^o Zatem: L=α+γ+x=α+γ+β+90^o=90^o+90^o=180^o L=α+β+y=α+β+γ+90^o=180^o, cnw. Czy moje rozwiązanie jest okej? Mam nadzieję że nie jest zbyt chaotycznie.

Saizou : Suma miar kątów w trójkącie wynosi 180=2(α+β+γ) → α+β+γ = 90 Trochę na wyrost ∡ADE = 90−β → ∡BDE = 180 − (90−β) = 90+β Analogicznie ∡CED = 90+γ ∡BCE + ∡BDE =α+γ+90+α = 180 ∡DBC + ∡CED =α+β+90+γ = 180 WNIOSEK: Na BCED można opisać okrąg

Szkolniak: Super, wszystko rozumiem, dzięki

Saizou : Zrobiłeś to samo, ale trochę na około, np. ∡ADE = 90−β prościej wynika z trójkąta prostokątnego ASD itd.

Szkolniak: Właśnie nie pomyślałem że przecież tam właśnie jest trójkąt prostokątny i z niego mogę coś pokombinować Tak samo przecież mogłem prościej ten warunek, że α+β+γ=90^o, tak jak Ty to zrobiłeś