geometria analityczna silly goose: W prostokątnym układzie współrzędnych OXY narysować zbiór Z={(x,y): x,y ∊R ∧ 2x² − y² ≥ 0} oraz znaleźć punkt tego zbioru położony najbliżej punktu M(1,4)

ite: Zacznij od narysowania 2x² − y² ≥ 0 → (√2x − y)(√2x + y) ≥ 0 Narysuj (√2x − y)(√2x + y)=0 i zaznacz odpowiednie półpłaszczyzny

silly goose: rozumiem, że mam narysować proste y=√2x i y=−√2x (?), ale nie wiem co zaznaczyć i co dalej

ite: Tak, trzeba narysować te proste. Każda z nich podzieli płaszczyznę na dwie półpłaszczyzny. Współrzędne punktów należących do jednej z półpłaszczyzn (bez brzegu) będą spełniać warunek x,y ∊R ∧ y>√2, dla drugiej prawdziwa będzie nierówność z mniejszością.

ite: Dalej trzeba ustalić dla jakich wartości x i y nierówność (√2x − y)(√2x + y) ≥ 0 jest prawdziwa.

ite: *uciekło x, poprawiam będą spełniać warunek x,y∊R ∧ y>√2*x

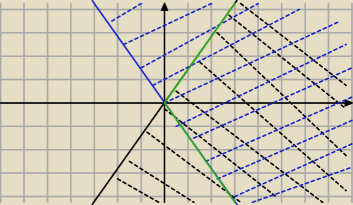
6latek: a*b≥0 ⇔(a≥0 i b≥0) lub (a≤0 i b≤0) √2x−y≥0 to y≤√2x √2x+y≥0 to y≥−√2x tam gdzie zielone sie pokrywaja razem z liniami to masz dla a≥0 i b≥0 √2x−y≤0 i √2x+y≤0

6latek: Ten przypadek zrob sam

silly goose: eeem na prostej y=√2x leży punkt najbliżej położony do M(1,4)? jak to policzyć? bo coś mi nie wychodzi

6latek: Najmniejsza odleglosc to bedzie mial punkt polozny na prostej prostopadlej do y=√2 i przecchodzacej przez punkt M

6latek: Piszesz rowmamie prostej prostopadlej do y=√2 i wyznaczasz punkt przeciecia tych prostych

silly goose: y=√2x a₁*a₂=−1

	−1		√2
a₂=		=−
	√2		2

	√2
4=		*1+b
	2

	8−√2
b=
	2

y=√2x

	−√2		8−√2
y=		x+
	2		2

wychodzi mi

	8√2−2
x=
	3

a w odpowiedziach jest

	4√2+1		8+√2
(		,		)
	3		3

co robię źle?

6latek: m=√2

	√2
m1= −
	2

Rownanie prostej prostopadlej do y=√2xi przechodzacej przez punkt M y₁= m₁(x−1)+4

	√2		√2
y1= −		x+		+4
	2		2

	√2		8+√2
y1= −		x+
	2		2

Sprawdz jeszcze raz swoje obliczenia

6latek: Wyjasnienie Ja znam postac rownania prostej przechodzacej przez dany punkt P=(x₀,y₀) y=a(x−x₀)+y₀ ===============

	√2
u nas a=−		x0=1 y0=4
	2

Jesli uczono Cie liczyc b to licz tak jak Cie uczono

silly goose: Już mam dobry wynik dziękuje za pomoc