Wyznacz pozostałe wierzchołki trójkąta. nervous: W trójkącie ABC dany jest wierzchołek A(1,2) oraz dane są równania dwóch dwusiecznych kątów wewnętrznych d1: 2x−y+3=0 i d2: x+y−1=0. Wyznacz pozostałe wierzchołki trójkąta.

chichi: d₁: 2x−y+3=0 ⇒ y=2x+3, d₂: x+y−1=0 ⇒ y=−x+1

	1		5		1		5
k⊥d1: a=−		, A∊k ⇒ b=		⇒ y=−		x+
	2		2		2		2

	⎧	y=2x+3
SAA' :	⎩	y=−1/2x+5/2	⇒ SAA'=(−1/5, 13/5)

	⎧	1+xA'=−2/5
A' :	⎩	2+yA'=26/5	⇒ A'=(−7/5, 16/5)

l⊥d₂: a=1, A∊l ⇒ b=1 ⇒ y=x+1

	⎧	y=−x+1
SAA'':	⎩	y=x+1	⇒ SAA''=(0, 1)

	⎧	1+xA''=0
A'' :	⎩	2+yA''=2	⇒ A''=(−1, 0)

	16   5
m: yA'A'' = yBC, a=		=−8 ⇒ b=−8 ⇒ y=−8x−8
	−2   5

	⎧	y=−8x−8
B:	⎩	y=−x+1	⇒ B=(−9/7, 16/7)

	⎧	y=−8x−8
C:	⎩	y=2x+3	⇒ C=(−11/10, 4/5)

Sprawdź czy nie machnąłem się gdzieś w obliczeniach

Mila: Dobrze

nervous: Zgadza się z odpowiedziami, dziękuję! Tylko nie rozumiem do końca na jakiej zasadzie jest m liczone

Mila: Poczekaj na chichi. Może miałby pretensję, że tłumaczę jego rozwiązanie. Jeśli nie wyjaśni, to napiszę

chichi: To prosta, na której leżą punkty A' i A'', więc wyznacam równanie prostej przechodzącej przez 2

	yA'−yA''
punkty, a=		, no a później podstawiam współrzędne punktu A' do
	xA'−xA''

wyliczenia 'b', bo obliczenia na jego współrzędnych są przyjemniejsze

getin: Jeśli nie wiesz jak wylicza się m to możesz wykorzystać wzór z tablic str. 5 Proste o równaniach kierunkowych y = a₁x+b₁ oraz y = a₂x+b₂ tworzą kąt ostry α taki, że:

	a1−a2
tg α = |		|
	1+a1*a2

d1 czyli y=2x+3 to dwusieczna kąta ABC d2 czyli y=−x+1 to dwusieczna kąta ACB Niech S będzie punktem przecięcia dwusiecznych d1 i d2 Wówczas kąty ACS = BCS = α kąty ABS = CBS = β Niech punkt B = (b, 2b+3) należy do dwusiecznej y=2x+3 C = (c, −c+1) należy do dwusiecznej y = −x+1 Współczynniki kierunkowe prostych BS i CS są równe a_BS = 2 a_CS = −1 Współczynniki kierunkowe prostych AB, BC, AC wyliczamy na podstawie wzoru a =

	y2−y1
	x2−x1

i podanych wierzchołków A = (1,2), B = (b, 2b+3), C = (c, −c+1)

	2b+1
aAB =
	b−1

	2b+c+2
aBC =
	b−c

	c+1
aAC =
	1−c

i teraz z tego wzoru z tablic

	a1−a2
tg α = |		|
	1+a1*a2

mamy równania

	aAC−aCS
tg α = |		|
	1+aAC*aCS

	aBC−aCS
tg α = |		|
	1+aBC*aCS

	aAB−aBS
tg β = |		|
	1+aAB*aBS

	aBC−aBS
tg β = |		|
	1+aBC*aBS

wówczas wychodzimy na układ równań

	aAC−aCS		aBC−aCS
{ |		| = |		|
	1+aAC*aCS		1+aBC*aCS

	aAB−aBS		aBC−aBS
{ |		| = |		|
	1+aAB*aBS		1+aBC*aBS

nervous: o jeny znam ten wzór na a, a jednak nie skojarzyłem, chyba ze zmęczenia Dziękuję za wyjaśnienia i pokazanie drugiego sposobu

Mila: nervous To już wszystko jasne? Wiesz dlaczego chichi szukał punktów symetrycznych do punktu A względem dwusiecznych?

Mila: getin myślałam o sposobie, który zaproponowałeś, ale za dużo niewiadomych. Sposób chichi przyjaźniejszy do obliczeń (według mnie).

getin: No dokładnie, bo w moim rozwiązaniu trzeba kombinować, wychodzi kilka rozwiązań i trzeba je odrzucać bo się np. okaże że punkty A B i C leżą na jednej prostej. A że z geometrii cienki jestem i ja np. w ogóle nie widzę tych A' oraz A'' to zaproponowałem typowe podejście na wzorach. Pozdrawiam

Mila: Czy mam wyjaśnić , gdzie te punkty są ?

getin: Poproszę wyjaśnić, chętnie zobaczę

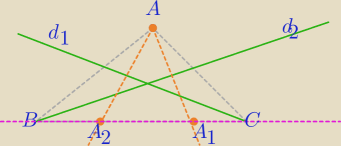
Mila: d₂− dwusieczna kąta B d₁− dwusieczna kąta C A− jeden z wierzchołków trójkąta Punktowi A odpowiada na drugim ramieniu kąta B taki punkt A₁, że ΔABA₁ jest Δrównoramiennym, a dwusieczna zawiera się w wysokości tego Δ. A₁ jest symetryczny do A względem dwusiecznej kąta B. Analogicznie A₂ odpowiada punktowi A na drugim ramieniu kąta C i ΔACA₂ jest Δ równoramiennym. Prosta A₁A₂ zawiera bok BC . Dalej wiadomo.

chichi: Cześć @Mila wprost z definicji dwusiecznej kąta

getin: Mila dzięki wielkie za wyjaśnienia. Już wiem o co chodzi, po prostu wyliczymy punkty A₂ i A₁ i się okaże że prosta A₁A₂ to jest prosta BC więc potem łatwo już wierzchołki B i C obliczymy odpowiednimi układami równań

Mila: chichi, getin . Dokładnie tak