Potrzebuję pomocy :/ Asia: Oblicz pole powierzchni całkowitej i objętość ostrosłupa prawidłowego sześciokątnego, którego pole podstawy jest równe 6√3, a wysokość ściany bocznej ma długość równą 3√3.

Jerzy: Potrafisz obliczyć krawędź podstawy ?

6latek:

	3a2√3
Pp=		i a>0
	2

2P_p= 3a²√3 3a²√3=2P_p

	2Pp
a2=
	3√3

	12√3
a2=		= 4 stad a=2
	3√3

6latek:

	a√3
ht=
	2

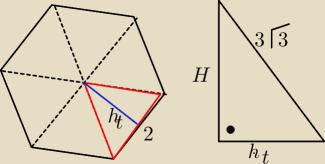
	2√3
ht=		= √3 = wysokosc trojkata rownobocznego w podstawie potrzebna bedzie do
	2

obliczenia wysokosci ostroslupaa H=√(3√3)²−h_t²= √18=3√2

	1		1
V=		Pp*H=		*6√3*3√2= 6√6
	3		3

Obliczamy pole powierzchni calkowitej a) obliczamy pole powierzchni jednej sciany bocznej P_sb a=2 h=3√3 P_sb=1*3√3=3√3 b) obliczamy pole powierzchni 6 scian bocznych P_pb P_pb=6*p_sb=18√3 c) obliczany pole powierzchni calkowitej P_c P_c=P_p+P−pb P_c=6√3+18√3=24√3

błąd: H= 2√6

6latek: A i owszem zamiast (√3)² liczylem 3² Ale to sobie poprawi