geometria analityczna
silly goose: Przez punkty A(2,1) i B(1,3) poprowadzono dwie różne proste równoległe
wyznaczające na osi OY odcinek o długości 2. Napisać równania tych prostych.
17 mar 18:59
kerajs:
1=2a+b1 ∧ 3=a+b2 ∧ |b1−b2|=2
17 mar 20:28
Mila:
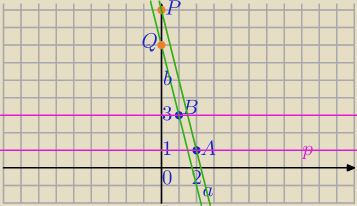
A(2,1) i B(1,3)
y=ax+b
1)a=0 to mamy proste:
y=1 i y=3
2)
a≠0
y=ax+b
A∊prostej a ⇔y=ax+1−2a
B∊prostej b⇔y=ax+3−a
P=(0,1−2a) punkt przecięcia z OY
Q=(0,3−a) punkt przecięcia z OY
|QP|=|3−a−1+2a|=|2+a|
|2+a|=2
2+a=2⇔a=0 i dwie proste (punkt 1)
lub
2+a=−2
a=−4
a: y=−4x+9
b: y=−4x+7
17 mar 21:03
silly goose: Dziękuje

17 mar 21:42
 A(2,1) i B(1,3)
y=ax+b
1)a=0 to mamy proste:
y=1 i y=3
2)
a≠0
y=ax+b
A∊prostej a ⇔y=ax+1−2a
B∊prostej b⇔y=ax+3−a
P=(0,1−2a) punkt przecięcia z OY
Q=(0,3−a) punkt przecięcia z OY
|QP|=|3−a−1+2a|=|2+a|
|2+a|=2
2+a=2⇔a=0 i dwie proste (punkt 1)
lub
2+a=−2
a=−4
a: y=−4x+9
b: y=−4x+7
A(2,1) i B(1,3)
y=ax+b
1)a=0 to mamy proste:
y=1 i y=3
2)
a≠0
y=ax+b
A∊prostej a ⇔y=ax+1−2a
B∊prostej b⇔y=ax+3−a
P=(0,1−2a) punkt przecięcia z OY
Q=(0,3−a) punkt przecięcia z OY
|QP|=|3−a−1+2a|=|2+a|
|2+a|=2
2+a=2⇔a=0 i dwie proste (punkt 1)
lub
2+a=−2
a=−4
a: y=−4x+9
b: y=−4x+7
