wyznacz najmniejszą i największą wartość funkcji
szarik: Wyznacz wartości (o ile istnieją) funkcji f: największą i najmniejszą w podanym zbiorze:
| | 10x | |
c) f(x)= |
| x∊(0,10) |
| | x2+1 | |
| | 1 | |
d) f(x)= |
| x∊<1,2) ∪ (2,3> |
| | x2−4 | |
| | 0 | |
W punkcie c obliczyłam granicę i wyszło limx→0+f(x)= |
| =0 |
| | 1 | |
ekstrema wyszły f
max(1)=5
i nie wiem co teraz. Największa wartość to 5, a najmniejsza? W odpowiedziach jest napisane że
nie istnieje, ale dlaczego?
16 mar 10:27
piotr: najmniejsza nie istnieje, bo dla kazdej wartości funkcji f(x), x∊(0,10) można podać mniejszą
16 mar 10:38
janek191:
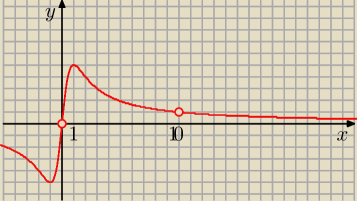
Przedział ( 0, 10 ) jest otwarty.
16 mar 10:39
piotr: np. : f(0.000001)< f(0.00001), f(9.999999)<f(9.99999)
16 mar 10:40
szarik: A punkt d? Co jeśli jest suma przedziałów?
17 mar 08:38
janek191:
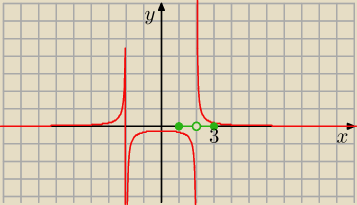
17 mar 09:05
szarik: janek191 dziękuję

17 mar 09:16
F&M: Ale to chyba wystarczy policzyć pochodną:
| | 2x | |
f'(x)= |
| i zauważyć, że zeruje się tylko dla x=0, a ten przecież nie należy do |
| | (x2−4)2 | |
dzidziny.
Wobec tego funkcja nie ma ekstremów lokalnych.
17 mar 09:25
ICSP: Mylisz pojęcie ekstremów lokalnych funkcji z wartością najmniejszą największą na danym zbiorze.
Zachowanie globalne funkcji nie ma większego wpływu na jej zachowanie lokalne.
Pochodna to tylko narzędzie −> poza tym, że powinna być używana rozsądnie to ponadto nie
rozwiąże wszystkich problemów.
Tak samo jest z "świętą Δ"
17 mar 09:34
F&M: Ok racja, ale to tutaj w takim razie należałoby by policzyć granicę do ,,2'' z obu stron
i wartości f(1) i f(3) ?
17 mar 09:53
ICSP: granice by wystarczyły.
17 mar 09:58
F&M: Ok.
17 mar 10:02
 Przedział ( 0, 10 ) jest otwarty.
Przedział ( 0, 10 ) jest otwarty.

