pochodna maturalnyy:

	kx4
Funkcja f(x)=		, x∊R jest rosnaca dla:
	x2+2

A. k∊(−∞;−2) B. k∊(−2;0) C. k>0 D. k∊R

	2kx5+8kx3
Policzyłem pochodna funkcji i mam f'(x)=		i teraz zrobilem tak f'(x)>0
	(x2+2)2

	2kx5+8kx3
		>0
	(x2+2)2

2kx⁵+8kx³>0 2kx³(x²+4)>0 2kx³>0 I co dalej?

maturalnyy: i zastanawialem sie tak ze dla k<0 ona bedzie rosla (−∞,0> a dla k>0 bedzie rosla <0,∞)

ICSP:

	x4
g(x) =
	x2 + 2

Funkcja g ma minimum lokalne w x = 0, dla x < 0 jest malejąca a dla x > 0 jest rosnąca. Nie ważne, przez jaką liczbę przemnożysz wartości funkcji g jej monotoniczność nie zmieni się na tylko rosnącą, albo tylko malejącą.

maturalnyy: czyli mam rozumiec ze nie ma poprawnej odpowiedzi?

Jerzy: Nie ma.

maturalnyy: nie polecam w takim razie zbiorow wydawnictwa Omega blad na bledzie tu jest

6latek: Dzien dobry Jerzy

Jerzy: Na marginesie, zauważ,że dla dowolnego k funkcja jest funkcją parzystą, a więc wykres jest symetryczny względem osi OY , a więc funkcja nie może być stale rosnąca lub malejąca.

Jerzy: Cześć Krzysztof

6latek: Spokojnie . jaki masz ten zbior ? czy to Zbior zadan maturalnych z matematyki na ocene celujaca Witold Stachnik? jesli tak to ktory numer zadania ?

Jerzy: Oczywiście poza: k = 0

6latek: Jerzy Zastanawiam sie tylko czy to nie bedzie odp d) Dlaczego ? Bo wedlug mnie nie jest napisane scisle rosnaca Czy wedlug Ciebie ma to jakies znaczenie ?

maturalnyy: to jest zbior arkuszy egzaminacyjnych nie ma tam tego pana

Jerzy: Dla dowolnego k ≠ 0 , ta funkcja jest monotoniczna w przedziałach (−∞,0) oraz (0,∞) Funkcja parzysta nie może być ściśle rosnąca/malejąca. Gdybya k = 0 , to funkcja nadal byłaby parzysta, ale stała.

6latek: Przyjąlem do wiadomosci

chichi: @6latek jeśli k∊R, to k=0 również, a wtedy mamy funkcję f(x)=0, czy ona kiedykolwiek rośnie? Nawet jeśli jest monotoniczna przedziałami, to wtedy trzeba podać przedział na jakim ta funkcja rośnie − przedział zależny od argumentów, nie od parametru, pozdrawiam

6latek: Witam

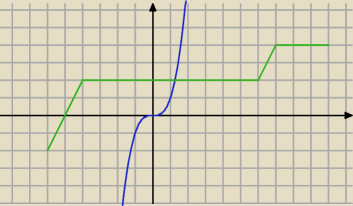
Jerzy: Krzysztof. Nibieska : ścilśe rosnąca. Zielona: niemalejąca.

6latek: Juz teraz rozumiem Miłego dnia

Jerzy: