Kombinacje 1_1 2_2 3_3 marek: Witam, nie wiem zabradzo gdzie to napisać. Potrzebuje wszystkie możliwe kombinacje dla 1−1 2−2 3−3 W stylu 1−1 2−2 3−3 1−1 2−3 3−2 itd. ja się.pogubilem trochę i moze ktoś bystrzejszy ogarnie 🙂

Jerzy: Podaj treść zadania, bo " w stylu" nie jest terminem matematycznym.

ICSP: Wpisz w google "permutacja". Poniższy link powinien pomóc: http://www.math.us.edu.pl/~pgladki/faq/node109.html

marek: Jerzy, to nie jest zadanie. Mam trzy kable z takim samym kolorem które zostały rozcięte i muszę je połączyć ze sobą i nie chce powtarzać tych samych połączeń i mieć listę możliwych łączeń

ICSP: (ilość kabli)! Masz wzór podany w linku o 13:57

F&M: No wszystkich jest 720, więc ciężko może być wypisać.

ICSP: a wszystkie możliwe kombinacje są następujące: (1,2,3) (1,3,2) (2,1,3) (2,3,1) (3,1,2) (3,2,1)

F&M: A, chodziło o 3 kable...nvm

Jerzy: Nie do końca rozumiem, ale jeśli kabel rozetniesz na trzy odcinki i oznaczysz je: A,B,C , to: A,B,C − trzy kable. Możliwe połączenia to 3! ( permutacje) , czyli 6 możliwości: ABC , ACB , BAC, BCA , CAB , CBA

Jerzy: 14:30 , to są raczej permutacje, a nie kombinacje.

Jerzy: Wpis 14:39 dotyczy @ICSP , te 6 nawiasów to jest jedna kombinacja.

marek: Dokładne e chodzi o to że są 3 kable, ktoś mądry je przeciął i one są oznaczone tym samym kolorem a zasilają co innego. Muszę znaleźć pasujące do siebie i tu szukam możliwych kombinavji

Jerzy: Dalej nic nie wiadomo. Masz trzy kable w jednym kolorze i ktoś je przeciął ( na ile kawałków ?) Co oznacza "pasujące do siebie" ?

Qulka: 3! 1z1 2z2 3z3 1z1 2z3 3z2 1z2 2z1 2z3 1z2 2z3 3z1 1z3 2z1 3z2 1z3 2z2 3z1

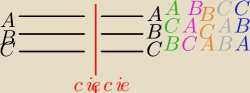
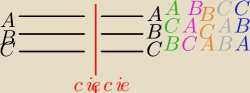Qulka: sześć