pole koła xxx: Punkt S = (− 1,5) jest środkiem okręgu wpisanego w trójkąt ABC , w którym A = (− 4,− 6) i B = (5,− 3) . Oblicz pole koła wpisanego w trójkąt ABC .

getin:

	1		14
1. Wyznacz równanie prostej AB (powinno wyjść y =		x−		)
	3		3

2. Wyznacz równanie prostej prostopadłej do prostej AB i przechodzącej przez S = (−1,5) − powinno wyjść y = −3x+2

	1		14
3. Oznacz punkt przecięcia prostych y =		x−		i y = −3x+2 np. jako K i układem
	3		3

równań z tych prostych wylicz współrzędne K (powinno wyjść K = (2, −4)) 4. Oblicz długość odcinka KS − będzie to promień koła (powinno wyjść √90) 5. Obliczamy pole koła − wyjdzie P = 90π

Eta: r=d , gdzie d−− odległość S od prostej AB

	1
aAB=
	3

	1
AB: y=		(x+4)−6
	3

AB : x−3y−14=0

	|−1−15−14|
d=r=		⇒ r2= 90
	√10

P_k=90π ====== i po ptokach

Eta: @xxx Jasne?

xxx: jasne jak najbardziej, dziękuję za pomoc

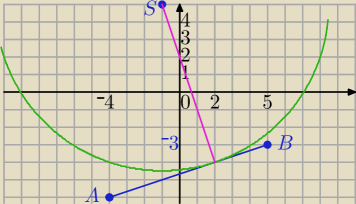
Mila: A = (− 4,− 6) i B =(5,− 3) S = (− 1,5) Prosta AB x−3y−14=0

	|−1−3*5−14|		30		30√10
d(S, AB)=		=		=		=3√10
	√1+9		√10		10

r=3√10 Czy to możliwe?

Eta: r=|AB| coś nie tak z danymi w treści Taki okrąg nie istnieje

getin: faktycznie się nie zgadza