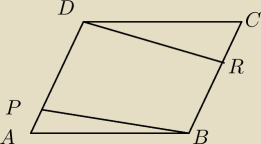
Pole czworokąta PBRD jest równe? zachód: Pole równoległoboku ABCD jest równe 120. Na bokach AD i BC wybrano − odpowiednio − punkty P i R, takie, że |AP|/|PD| = 1/3 |CR|/|RB|=2/3. Pole czworokąta PBRD jest równe?

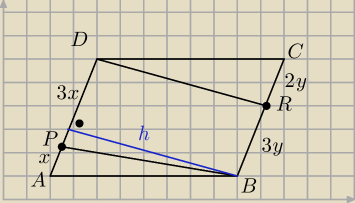Saizou : 4x = 5y

	4
y =		x
	5

	30
120 = 4x*h →h =
	x

	1		1		30
PABP =		hx =		*		*x = 15
	2		2		x

	1		30		4
PCDR =		h*2y = hy =		*		x = 24
	2		x		5

zatem...

zachód: P= 81 thanks

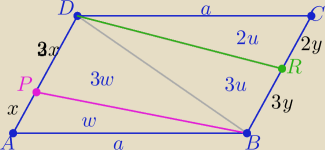Eta: w, 3w,2u,3u −− pola trójkątów 4w=60 ⇒ w=15 i 5u=60 ⇒ u=12 P(PBRD)= 3w+3u=3(w+u)= 3*27 = 81