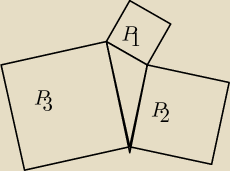
Wykaż, że P1+P2> u{1}{2}P3 silly goose: Na bokach trójkąta zbudowano kwadraty o polach P1, P2 i P3. Wykaż, że P1+P2> ¹₂P3

ICSP: a − bok trójkąta 1 b − bok trójkąta 2 c − bok trójkąta 3 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	a2 + b2		a + b		c
(		)1/2 ≥		>
	2		2		2

	a2 + b2		c
(		)1/2 >		//2
	2		2

a2 + b2		c2
	>		// *
2		4

	1
a2 + b2 >		c2
	2

silly goose: sorki ale nic z tego nie rozumiem co to jest to (^{a2 + b2}₂) ¹₂?

Saizou :

	a2+b2		a2+b2
(		)1/2 = √
	2		2

Nierówność między średnią kwadratową a arytmetyczną

	a2+b2		a+b
√		≥
	2		2

Korzystamy z nierówności trójkąta, tzn. a+b>c. Ułamek zmniejszymy zmniejszając licznik, zatem

	a2+b2		a+b		c
√		≥		>
	2		2		2

Reszta to kwestia przekształceń

ICSP: Średnia kwadratowa liczb a i b Średnia kwadratowa jest większa lub równa od średniej arytmetycznej. Więcej tutaj: http://www.math.edu.pl/wartosci-srednie Druga nierówność wynika z własności trójkąta(a + b > c) Od drugiej linijki pod kreską zaczyna się zwykła algebra.

silly goose: Dziękuje już rozumiem, ale sama bym nigdy na to nie wpadła

Biedroneczki są w kropeczki: A bez średnich?

ICSP:

	1		1		1
P = a2 + b2 =		[(a+b)2 + (a−b)2] ≥		(a+b)2 >		c2 = L
	2		2		2

Jednak zostałbym przy rozwiązaniu wykorzystującym zależność K₂ ≥ A₂

Biedroneczki są w kropeczki: Dziekuje .