Znaleźć równanie osi symetrii figury będącej sumą prostych nervous: Znaleźć równanie osi symetrii figury będącej sumą prostych: l: x + y − 3 = 0 i k: 7x − y + 4 = 0 odp. 2x−6y+19=0 i 12x +4y−11 Nie wiem co oznacza i jak wygląda figura będąca sumą prostych, proszę o pomoc

ICSP: suma prostych to X mniej lub bardziej spłaszczony. Oczywiście jeśli nie są równoległe.

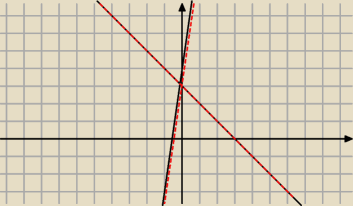
6latek: To na czerwono to suma tych prostych

nervous: przekształcam proste na: l: y=−x+3 k: y=7x+4 mam nawet punkt wspólny: (−¹₈, ²⁵₈) więcej nie potrafię zrobić Jak znaleźć osie symetrii?

janek191: Jest wzór na dwusieczną kąta.

janek191: Jeżeli proste : m: A₁ x+ B₁ y + C₁ = 0 n: A₂ x +B₂ y + C₂ = 0 nie są równoległe, to dwusieczne d₁ i d₂ kątów utworzonych przez te proste spełniają równanie:

I A1 x + B1 y + C1I		I A2x+ B2 y +C2I
	=
√A12 + B12		√A22 + B2

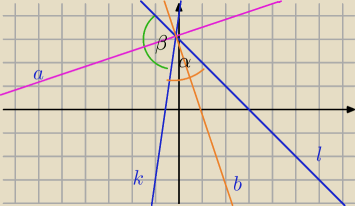
Mila: l: x + y − 3 = 0 lub k: 7x − y + 4 = 0 l: y=−x+3 k: y=7x+4 Równanie osi symetrii figury składającej się z dwóch prostych. Będą dwie osie symetrii: dwusieczne kątów między prostymi. 1) P=(x,y) − punkt należący do dwusiecznej kąta α, β Każdy punkt dwusiecznej kąta jest jednakowo odległy od ramion kąta

|x+y−3|		|7x−y+4|
	=		⇔
√12+12		√72+12

|x+y−3|		|7x−y+4|
	=		⇔
√2		√50

5|x+y−3|=|7x−y+4| rozwiązuj sam 2) Wynik: dwie prostopadłe:

	1		19
a: y=		x+
	3		6

lub

	11
b: y=−3x+
	4

6latek: Dobry wieczor Ogolnie to należy postac ogolna proste doprowadzić do postaci normalnej i je przyrownac do siebie (raz ze znakiem + a drugi raz ze znakiem (−) ) Milu okazało się ze wczoraj jednak zle odczytałem to równanie trygonometryczne i dlatego zle wychodzilo .

nervous: Dziękuje bardzo za pomoc, wszystko wyszło

Mila:

Mila: Zauważyłam 6−latku. Nie przejmuj się.