Zbadaj czy istnieje granica Artur : Zbadaj czy istnieje granica lim → ∞ sin x

Adamm: Nawet lepiej. Można udowodnić że ciąg sin(n) jest gęsty w [−1, 1] tzn. jego punkty skupienia to cały odcinek [−1, 1]

Artur : Czyli z tego wynika ,że nie istnieje? Bo muszę jakoś to udowodnić.

Artur : Sory tu miało być lim → −∞

6latek: Nie istnieje Rozwaz dwa ciagi okreslone nastepujaco

	π
xn=nπ i drugi ciag xn=		+2nπ in=1,2,3,......
	2

Adamm: W szczególności nie istnieje

Artur : Dobrze ale czy lim → −∞ Będę musiał rozwiązać jako dwa ciągi ? czy to będzie ∞ i − ∞ czy to nic nie zmieni?

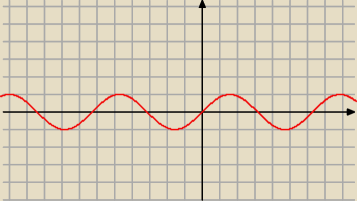
Adamm: Rozumiesz pojęcie granicy funkcji w +−nieskończoności ? Chodzi o to jak zachowują się wartości funkcji gdy jej argumenty są bardzo duże lub bardzo małe. Argumenty to x a wartości to y. Tutaj y = sin(x). Narysuj go sobie lub wyobraź.

Artur : No nie do końca właśnie rozumiem dlatego tutaj pytam o to zdanie

Jerzy: Zauważ,że niemal identycznie zachowuje się ta funkcja, gdy x → − ∞