algebra liniowa salamandra: Wyznaczyć równania wektorowe i parametryczne prostej: a) przechodzącej przez punkt (2,0,5) i równoległej do wektora (4,2,11) wektorowe: (2,0,5)+t[4,−2,11] parametryczne: x1=2+4t x2=−2t x3=5+11t nie wiem co zrobić z tą równoległością?

Jerzy: Nic,tylko postać parametryczną zapisać tak: x = 2+4t y = −2t z = 5 + 11t

salamandra: dzięki

salamandra: A co w przypadku, gdy mam b) przechodzącej przez punkty (−1,2,1) i (2,−3,2) Jak takie coś zacząć? Nie mogę się nigdzie doszukać, bo wyskakują mi tylko wyjaśnienia dla "normalnych" prostych ze szkoły średniej.

ICSP: a te proste to już nie są normalne ? p = A + (BA)t, t∊R gdzie A,B to punkty należące do prostej a BA to wektor o początku w punkcie A i końcu w punkcie B

salamandra: znalazłem taki wzór:

x−x1		y−y1		z−z1
	=		=		=t
x2−x1		y2−y1		z2−z1

czy jest on właściwy do tego zadania?

Kacper: ICSP czym się zajmujesz? pytam tak z ciekawości?

Mila: Równanie prostej przechodzącej przez punkty A= (−1,2,1) i B=(2,−3,2). AB^→[3,−5,1] 1) Równanie prostej:

x+1		y−2		z−1
	=		=
3		−5		1

k^→=[3,−5,1]− wektor kierunkowy prostej 2) Równanie parametryczne : x=−1+3t y=2−5t z=1+t, t∊R

salamandra: też właśnie do tego doszedłem, ale moje pytanie brzmi jeszcze: dlaczego, gdy zapisuję równanie w postaci wektorowej: k: (−1,2,1)+t[3,−5,1] to na początku jest punkt A, a nie punkt B? czy mógłby tam być równie dobrze punkt B i "odwrotny" wektor?

Mila: Możesz wstawić wsp. punktu B

x−2		y+3		z−2
	=		=
3		−5		1

Do równania parametrycznego tak samo . Możesz też wstawić dowolny wektor równoległy do AB np. [6,−10,2] To będzie ta sama prosta. Zwykle wstawia się po uproszczeniu.

salamandra:

	y+3
wtedy nie będzie		?
	5

Mila: Wektor przeciwny miałeś na myśli? [−3,5,−1] || [3,−5,1]

salamandra: tak, jeśli za x₂ przyjąłbym punkt A, a za x₁ punkt B i wyszłyby mi de facto dwa różne równania, to czy opisują one nadal tę samą prostą?

Mila: Najlepiej wpisz zadania, to wszystko się wyjaśni praktycznie. Wpisz swoją wersję, to odpowiem.

salamandra: W sumie to postaram się na tym samym zadaniu: A=(2,−3,2) B=(−1,2,1) BA−>=[−3,5,−1] y: (2,−3,2)+t[−3,5,−1] parametrycznie: x=2−3t y=−3+5t z=2−t Czy to jest równoważne z tym, co napisałaś 20:25?

Mila: Ta sama prosta : −1+3s=2−3t 2−5s=−3+5t 1+s=2−t ======= s=1−t podstawiamy do (1) −1+3(1−t)=?2−3t 2−3t=2−3t, 0=0 do (2) L=2−5(1−t)=−3+5t=P Ta sama prosta:

salamandra: super, dziękuję, mam jeszcze pytanie, być może głupie, ale nie miałem jeszcze wykładu z tego, a ćwiczenia wyprzedzają wykład − czym jest tak naprawdę ten parametr "t"? Czy jest to coś w stylu "b" w prostej ax+b? Że zmiana tego parametru powoduje, że to zupełnie inna prosta?

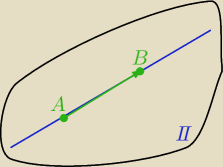
Mila: Parametr t ∊R Jeśli masz równanie prostej: x=2−3t y=−3+5t z=2−t to możesz wyznaczyć współrzędne punktów należących do tej prostej. dla t=0 masz punkt: (2,−3,2) t=1 (−1, 2,1) t=−1 (5,−8,3)

salamandra: rozumiem, dziękuję raz jeszcze

Mila: Ściągnij sobie w pdf Algebra liniowa 1 T. Jurlewicz, Z. Skoczylas. Tam jest geometria analityczna w R3.