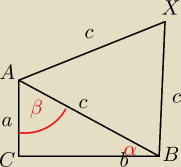
Trojkat Goblin: Na przeciwprostokatnej AB trojkata prostokatnego ABC zbudowano trojkat rownoboczny ABX Wyznaczyc kąty trojkata ABC jesli wiadomo ze pole trojkata ABX jest dwa razy wieksze od pola trojkata ABC β=90−α P_ΔABC=0,5ab P_ΔABX= 2*0,5ab=a*b z warunkow zadania

	c2√3
PABX=		ogolnie
	4

	c2√3
a*b=
	4

c2√3
	=a*b
4

√3		a*b
	=
4		c2

√3		a		b
	=		*
4		c		c

	a		b
Z trojkata ABC		=sinα i		=cosα
	c		c

√3
	= sinα*cosα
4

Dotąd doszedłem

ello: 2sinαcosα=sin(2α)

√3
	= sin(2α) ⇒ 2α=60o ⇒ α=30o β=60o
2

Goblin: No tak . dziekuje