pomoc z 2 zadaniami świetlik: witam prosze o pomoc z 2 zadaniami na ktore nie mam pomyslu 1. wykaz ze dla kazdej dodatniej i roznej od jenosci liczby a i dla kazdej dodatniej i roznej od jednosci liczby b spelnina jest rownosc 1/(log_a b)+1/(log_a² b)+1/(log_a³ b)+...+1/(log_a¹⁰ b)=55/(log_a b) 2.Trapez rownoramienny o przekatnej dlugosci 13cm i obwodzie rownym 48cm jest opisany na okregu. Oblicz dlugosc promienia okregu wpisanego w ten trapez oraz dlugosc promienia okregu opisanego na tym trapezie. Nie sa to zadania domowe wiec prosze sie nie spieszyc a chcialbym zobaczyc rozwiazanie zeby je jakos zrozumiec po przeczytaniu pare razy

chichi: (1)

	1
Skorzystajmy ze wzoru: logar (b) =		loga (b), a≠1 ∧ a>0 ∧ b>0
	r

1		1		r
	=		=		, zatem mamy:
logar (b)		1   loga (b) r		loga (b)

	1		1		1		1
L =		+		+		+
	loga (b)		loga2 (b)		loga3 (b)		loga10 (b)

	1+2+3+...+10		55
L =		=		= P
	loga (b)		loga (b)

Q.E.D.

Filip:

1		1		1
	+		+ ... +
logab		loga2b		loga10b

= log_ba + 2log_ba + ... + 10log_ba = 55log_ba

	55
=
	logab

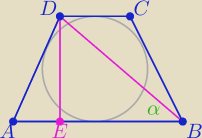chichi: (2) |DB|=13, |AB|=a, |CD|=b, |DE|=2r, L=48=a+b+2c Okrąg wpisany w trapez, zatem mamy: a+b=2c ⇒ L=4c=48 ⇒ c=12 ⇒ a+b=24 W ΔDEB:

	a+b		24		5
|EB|=		=		=12, zauważmy, że ΔDEB jest trójkątem (5,12,13) ⇒ 2r=5 ⇒ r=
	2		2		2

W ΔADB: Okrąg opisany na tym trójkącie jest również okręgiem opisanym na trapezie ABCD: sin(α)=5/13 Z tw. sinusów mamy:

12		78
	= 2R ⇒ R=
5   13		5