Planimetria
Kropka:
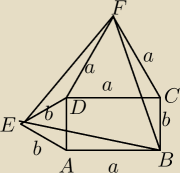
Dany jest prostokąt ABCD, na boku AD zbudowano trójkąt równoboczny i na boku DC także
zbudowano trójkąt równoboczny. Uzasadnij, że |EF| = |FB|
Czy mój sposób jest dobry?
Początkowo możemy zauważyć, że skoro trójkąt EAD i DCF są równoboczne, to mają 3 kąty po 60
stopni
Następnie połączyłem Wierzchołek E z B, dzięki czemu powstał mi trójkąt EBF,
następnie możemy zauważyć, że mamy 3 trójkąty przystające do siebie,
a dokładniej − EAB, BCF i EDF.
Te trójkąty są przystające ponieważ:
1) |kąt BCF| = 90 + 60 = 150 stopni
|kąt EAB| = 90 + 60 = 150 stopni
|kąt EDF| = 360 − 60 − 60 − 90 = 150 stopni
Dzięki temu wiemy, że każdy z tych trójkątów ma dwa boki a i b oraz kąt 150 stopni pomiędzy
nimi,
więc na podstawie cechy "bok−kąt−bok" te 3 trójkąty są przystające, czyli ten 3 bok możemy
oznaczyć jako "C"
|EB| = c, |BF| = c, |EF| = c ===> Jest to trójkąt równoboczny, czyli |EF| = |FB|
Czy wszystko jest dobrze? Jest jakiś inny lepszy/szybszy sposób?
9 mar 20:04
ello:
OK
9 mar 20:34
Mila:
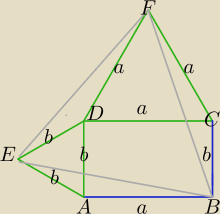
1) ΔEAB≡ΔBCF cecha bkb (a,150
o,b )⇔|EB|=|BF|
2) W ΔEDF:
|∡EDF|=360
o−(60
o+60
o+90
o)=150
o⇒
ΔEDF≡ΔEAB≡ΔBCF
|EF|=|FB|
Możesz zaznaczyć miary kątów na rysunku,
wtedy mniej czasu zajmie Ci pisanie komentarzy.
9 mar 22:08
ello:
Ładnie opisał

9 mar 22:17
Mila:
Kropka Opisał ładnie, ale może mu brakować czasu.
O ile wzór Picka może być problematyczny,
to do zaznaczonych kątów w Δ równobocznych nie będzie zastrzeżeń.
9 mar 22:21
 Dany jest prostokąt ABCD, na boku AD zbudowano trójkąt równoboczny i na boku DC także
zbudowano trójkąt równoboczny. Uzasadnij, że |EF| = |FB|
Czy mój sposób jest dobry?
Początkowo możemy zauważyć, że skoro trójkąt EAD i DCF są równoboczne, to mają 3 kąty po 60
stopni
Następnie połączyłem Wierzchołek E z B, dzięki czemu powstał mi trójkąt EBF,
następnie możemy zauważyć, że mamy 3 trójkąty przystające do siebie,
a dokładniej − EAB, BCF i EDF.
Te trójkąty są przystające ponieważ:
1) |kąt BCF| = 90 + 60 = 150 stopni
|kąt EAB| = 90 + 60 = 150 stopni
|kąt EDF| = 360 − 60 − 60 − 90 = 150 stopni
Dzięki temu wiemy, że każdy z tych trójkątów ma dwa boki a i b oraz kąt 150 stopni pomiędzy
nimi,
więc na podstawie cechy "bok−kąt−bok" te 3 trójkąty są przystające, czyli ten 3 bok możemy
oznaczyć jako "C"
|EB| = c, |BF| = c, |EF| = c ===> Jest to trójkąt równoboczny, czyli |EF| = |FB|
Czy wszystko jest dobrze? Jest jakiś inny lepszy/szybszy sposób?
Dany jest prostokąt ABCD, na boku AD zbudowano trójkąt równoboczny i na boku DC także
zbudowano trójkąt równoboczny. Uzasadnij, że |EF| = |FB|
Czy mój sposób jest dobry?
Początkowo możemy zauważyć, że skoro trójkąt EAD i DCF są równoboczne, to mają 3 kąty po 60
stopni
Następnie połączyłem Wierzchołek E z B, dzięki czemu powstał mi trójkąt EBF,
następnie możemy zauważyć, że mamy 3 trójkąty przystające do siebie,
a dokładniej − EAB, BCF i EDF.
Te trójkąty są przystające ponieważ:
1) |kąt BCF| = 90 + 60 = 150 stopni
|kąt EAB| = 90 + 60 = 150 stopni
|kąt EDF| = 360 − 60 − 60 − 90 = 150 stopni
Dzięki temu wiemy, że każdy z tych trójkątów ma dwa boki a i b oraz kąt 150 stopni pomiędzy
nimi,
więc na podstawie cechy "bok−kąt−bok" te 3 trójkąty są przystające, czyli ten 3 bok możemy
oznaczyć jako "C"
|EB| = c, |BF| = c, |EF| = c ===> Jest to trójkąt równoboczny, czyli |EF| = |FB|
Czy wszystko jest dobrze? Jest jakiś inny lepszy/szybszy sposób?
 1) ΔEAB≡ΔBCF cecha bkb (a,150o,b )⇔|EB|=|BF|
2) W ΔEDF:
|∡EDF|=360o−(60o+60o+90o)=150o⇒
ΔEDF≡ΔEAB≡ΔBCF
|EF|=|FB|
Możesz zaznaczyć miary kątów na rysunku,
wtedy mniej czasu zajmie Ci pisanie komentarzy.
1) ΔEAB≡ΔBCF cecha bkb (a,150o,b )⇔|EB|=|BF|
2) W ΔEDF:
|∡EDF|=360o−(60o+60o+90o)=150o⇒
ΔEDF≡ΔEAB≡ΔBCF
|EF|=|FB|
Możesz zaznaczyć miary kątów na rysunku,
wtedy mniej czasu zajmie Ci pisanie komentarzy.
