prawdopodobienstwo ola: Mamy dwie urny. W pierwszej jest 5 kul białych i 5 kul czarnych, w drugiej są 3 kule białe i 7 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z liczbą oczek podzielną przez 3, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe?

Jerzy:

	1		5		2		3
P(A) =		*		+		*
	3		10		3		10

F&M: Tu masz wyjaśnienie: A−wylosowanie kuli białej Warunki B_[1} i B₂" B₁−liczba oczek podzielna przez 3 B₂−liczba oczek niepodzielna przez 3 Wzór na prawdopodobieństwo całkowite: P(A)=P(A I B₁)*P(B₁)+P(A I B₂)*P(B₂)

	5		1		3
P(A I B1)=		=		, P(A I B2)=		,
	10		2		10

	2		1		4		2
P(B1)=		=		, P(B2)=		=
	6		3		6		3

	1		1		2		3		1		1		11
Podstawiamy do wzorku: P(A)=		*		+		*		=		+		=
	3		2		3		10		6		5		30

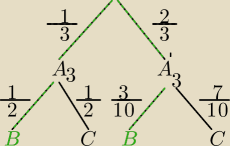
circle: U1 5B,5C U2 3B, 7C X={3,6}, X'={1,2,4,5} A₃− otrzymano liczbę ze zbioru X Przebieg doświadczenia losowego na drzewku.

	1		1		2		3
P(B)=		*		+		*
	3		2		3		10