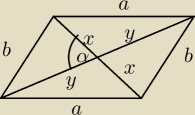
 W równoległoboku o bokach długości a i b, gdzie a > b,
kąt między przekątnymi ma miarę α, α ∈(0°, 90°).
Wykaż, że pole P tego równoległoboku jest równe 12(a2−b2)tgα.
b2=x2+y2−2xycosα
a2=x2+y2+2xycosα
W równoległoboku o bokach długości a i b, gdzie a > b,
kąt między przekątnymi ma miarę α, α ∈(0°, 90°).
Wykaż, że pole P tego równoległoboku jest równe 12(a2−b2)tgα.
b2=x2+y2−2xycosα
a2=x2+y2+2xycosα
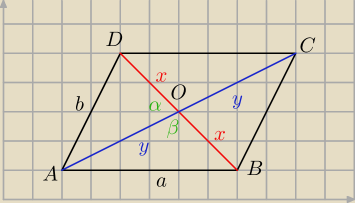 β = 180−α
W trójkącie AOD
1) Z tw. cosinusów
b2 = x2 + y2 − 2xycosα
β = 180−α
W trójkącie AOD
1) Z tw. cosinusów
b2 = x2 + y2 − 2xycosα
| 1 | ||
2) P1 = | xysinα | |
| 2 |
| 1 | 1 | |||
2) P2 = | xysinβ = | xysinα | ||
| 2 | 2 |
| 2P | ||
P = 2P1+2P2 = 2xysinα → 4xy = | ||
| sinα |
| 2P | ||
a2−b2 = | *cosα | |
| sinα |