prosze o pomoc aLLA: oblicz sinus jezeli cos= 12/13 2)oblicz cos jezeli tg= 4/3 3) sin alfa=cos alfa

Goblin:

	1
b) cosα=±
	√1+tg2α

a)sinα=±√1−cos²α

	π
3) sinα=cosα dla α=		+2kπ
	4

Jakub: moze ktos podac odpowieddzi, prosze bardzo///////////////////////////

Jerzy: 18:47, drugie źle.

Jerzy: Tzn. trzecie.

Jakub: jerzy podaj dobrze

Goblin:

	π
popraw na α=		+kπ
	4

masz do rozwiazania rownanie sinα= cosα sinα= sin(π/2−α)

	π
α=		−α+2kπ wylicz α
	2

	π
lub α=π−(		−α)+2kπ tez wylicz α (zobaczysz co wyjdzie
	2

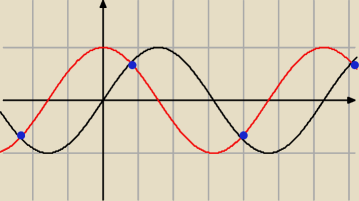
Goblin: czarny y=sin(x) czerwony y=cos(x)

Goblin: do nr 2

	sinα		√1−cos2α
tgα=		=		(obie strony do kwadratu
	cosα		cosα

	1−cos2α
tg2α=		(mnoze przez cos2α)
	cos2α

tg²α*cos²α=1−cos²α tg²α*cos²α+cos²α=1 cos²α(1+tg²α}=1

	1
cos2α=
	1+tg2α

	1
cosα=±		mamy zaleznosc cosinusa od tangensa
	√1+tg2α

===================== Tak samo mozna sobie wyprowadzic zaleznosc sinusa od tangensa

Jerzy:

	sinx		π
sinx = cosx ⇔		= 1 ⇔ x =		+ kπ
	cosx		4

ello:

	4		sinα		3
b) tgα=		=		⇒ sinα=		cosα
	3		cosα		4

z jedynki trygonometrycznej

	9		16
		cos2α+cos2α=1 ⇒ cos2α=
	16		25

	4
cosα= ±
	5