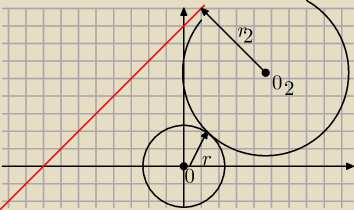
Krzywa srodkow okregow Goblin: 0₂=(x,y) *takie wspolrzedne 0=(0,0) prosta k (czerwona ) y=x+8 r=2√2 Rownanie prostej k w postaci ogolnej x−y+8=0 stad A=1 B=−1 C=8 Odleglosc punktu O₂ od prostej to dlugosc promienia r₂

	|1*x−1*y+8|		x−y+8
r2=		=
	√2		√2

	x−y+8
|OO2|= r+r2= 2√2+
	√2

Takze |OO₂|= √(x−0)²+(y−0)²=√x²+y² Mozemy napisac ze

	x−y+8
√x2+y2=2√2+		(mnoze obustromnie przez √2
	√2

√2x²+y²= 4+x−y+8 √2x²+y²=x−y+12 (podnosze obie strony do kwadratu 2x²+2y²= x²+y²+144−2xy+24x−24y x²+y²= 24x−24y+144−2xy (x+y)²−2xy=24x−24y+144−2xy (x+y)²=24x−24y+144 Ma to byc rownanie krzywej na ktorej leza srodki okregow stycznych do prostej i okregu o srodku (0,0) i r=2p[2}} Zastanawiam sie co to za krzywa

Saizou : hmm... nie sprawdzając rachunków, krzywa o równaniu (x+y)²=24x−24y+144 jest parabolą.

Goblin: Dobrze . Jak bys to przeksztalcil zeby to wygladalo na rownanie parabli w postaci ogolnej y=ax²+bx+c?

Goblin:

ICSP: Krzywa nie musi być funkcja.

Saizou : Dla krzywych stopnia drugiego(krzywych stożkowych) postaci Ax² + By² + Cxy + Dx + Ey + F = 0 (A≠0, B≠0 i C≠0, A, B, C, D, E, F ∊ R) definiuje się tak zwane niezmienniki, które nie ulegają zmianie podczas przekształceń zachowujących odległości (np. obrót czy przesunięcie). 2A C D W = det ( C 2B E ) D E 2F oraz 2A C w = det ( C 2B) Jeżeli W ≠ 0 i w = 0, to krzywa jest parabolą. U nas x²+y²+2xy−24x+24y−144 = 0 W = −4608 w = 0

Goblin: Dzięki .