całka Filip: Oblicz całkę podwójną po obszarze normalnym ∫∫(x + y²)dxdy, gdzie D jest obszarem ograniczonymi liniami x = y² i x = 2y D Czy dobrze zapisałem całke do policzenia? 0 <= x <= 4

1
	x <= y <= √x
2

wtedy mam całkę ₀∫⁴(_x/2∫^√x(x + y²)dy)dx = 1.2 W odpowiedziach mam 3.7

jc: 56/15

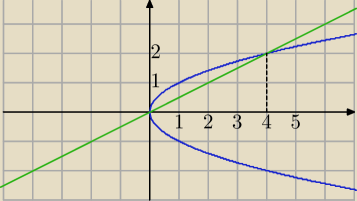Mila: ₀∫⁴[_y=(1/2)x∫^y=√x (x+y²)dy]dx=

	1
= 0∫4([xy+		y3}](1/2)x√x) dx=
	3

	4		x2		x3
=0∫4(		x3/2−		−		) dx=
	3		2		24

	8		x3		x4		56
=[		x5/2−		−		]04=
	15		6		24*4		15

Filip: Własnie tak liczyłem i mi tyle nie wyszło

Mila: Pewnie masz błąd rachunkowy

8		43		44
	*√45−		−		−0=
15		6		24*4

8		64		16		8*32		40		256		200
	*32−		−		=		−		=		−		=
15		6		6		15		3		15		15

	56
=
	15