Zestaw nr 1
Goblin: Zadanie nr 1
Dla jakiej wartosci parametru m rownanie
ma dokladnie jedno rozwiazanie ?.Znalezc to rozwiazanie
Zadanie nr 2
Okreslic zbior wszystkich srodkow okregow stycznych zewnetrznie do okregu wpisanego w trojkat o
wierzcholkach
A=(−
√3,0) B=(
√3,0) C=(0,−3)i stycznych do osi OX
naszkicowac te krzywa
Zadanie nr 3
W prostokatnym ukladzie wspolrzednych narysowac zbior A jesli
A={x,y) : log
x−y(x+y)≤1
Zadanie nr 4
Wsrod wszystkich trojkatow o danym kącie δ przy wierzcholku C i danej sumie d dlugosci bokow
wychodzacych z wierzcholka C wybrac taki, ktorego dlugosc boku lezacego naprzeciwko tego
wierzcholka jest najmniejsza
Zadanie nr 5
Z piewszej urny zawierajacej n kul czerwonych i trzy zielone losujemy dwie kule i wrzucamy je
do drugiej urny poczatkowo pustej .
Nastepnie z drugiej urny losujemy jedna kule .
Ile powinno byc kul czerwonych w pierwszej urnie ,aby prawdopodobienstwo wylosowania kuli
| | 7 | |
czerwonej z drugiej urny bylo mniejsze od |
| ? |
| | 12 | |
7 mar 09:33
7 mar 10:09
Saizou :
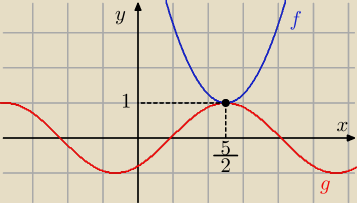
Zad. 1
| | 5 | |
Niech f(x) = x2−5x+6−m oraz g(x) = cos(x− |
| ) |
| | 2 | |
Funkcja g przyjmuje wartości ze zbioru [−1, 1]
Wykresem funkcji f jest parabola skierowana ramionami do gór.
Aby wykresy funkcji f i g przecinały się w jednym punkcie, spełnione muszą być warunki
y
w = 1
zatem
7 mar 10:16
7 mar 10:18
Goblin: Dzień dobry

. Sa to zestawy na egzaminy wstepne na SGH (co sumie na jedno wychodzi )

Dzięki
Saizou .
7 mar 10:34
Saizou :
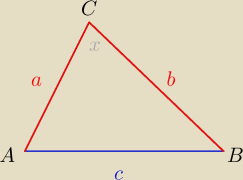
Jakoś tak

może ktoś potwierdzi

δ = x
a+b = d
d
2−2ab = a
2+b
2
Z nierówności między średnimi
Am ≥ Gm
Z tw. cosinusów
c
2 = a
2+b
2−2abcosx
c
2 = d
2−2ab−2abcosx
d
2(1+cosx) ≥ 2d
2−2c
2
7 mar 10:54
Goblin:
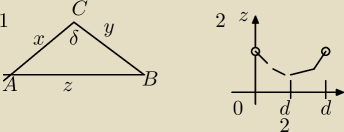 Saizou
Saizou
To zadanie nr 4 gościu akuratnie pokazał jak rozwiazac wiec
AC=x BC=y x+y=d δ∊(0,π) AB=z
wielkosci d i δ sa dane
Stosujac do ΔABC tw cosinusow mamy
z
2=x
2+y
2−2xycosδ
podstawiajac do tej rownosci y=d−x dostajemy
z
2=x
2+(d−x)
2−2x(d−x)*cosδ
lub w postaci rownowaznej
z=
√x2+(d−x)2−2x(d−x)cosδ=f(x)
W powyzszej rownosci x∊(0,d)
szukamy najmniejszej wartosci funkcji f(x) na zbiorze (0,d)
badamy w tym celu znak pochodnej funkcji f na przedziale (0,d)
Kolejno mamy
| | 2x+2(d−x)(−1)−2dcosδ+4xcosδ | |
f'(x)= |
| |
| | 2√x2+(d−x)2−2x(d−x)cosδ | |
| | 2x−2d+2x−2dcosδ+4xcosδ | |
= |
| |
| | 2√x2+(d−x)2−2x(d−x)cosδ | |
| | (1+cosδ)(4x−2d) | |
= |
| |
| | 2√x2+(d−x)2−2x(d−x)cosδ | |
Z warunku δ(0,π) wynika ze 1+cosδ>0
Zatem mamy
f'(x)>0⇔x∊(d/2,d)
f'(x)<0⇔x∊(0,d/2)
Z tych warunkow oraz z ciaglosci funkcji f na zbiorze (0,d) wynika ze
| | d | |
min x∊(0,d) f(x)=f( |
| ) wykres nr 2 |
| | 2 | |
| | d | | d | |
Jesli jednak x= |
| to y= |
| dostajemy stad AC=BC |
| | 2 | | 2 | |
Odp. Sposrod wszystkich trojkatow o danym kącie δ przy wierzcholku i danej sumie dlugosci bokow
wychodzacych z tego wierzcholka najkrotszy trzeci bok ma trojkat rownoramienny
Uwaga 1
| | d | |
Jesli funkcj f jest malejaca na (0,d/2) i rosnaca na (d/2,d) i nie jest ciagla w x= |
| |
| | 2 | |
to wartosc najmniejsza nie musi istniec
Uwaga 2
Jesli f jest okreslone na przedziale domknietym <0,d> oraz maleje (0,d/2)i rosnie w (d/2,d) to
wartosc najmniejsza funkcji f na przedziale <0,d> niekoniecznie musi wystapic w punkcie
Nie mozna zatem utozsamiac szukania ekstremum lokalnego funkcji f (na danym zbiorze A⊂D(f)) z
szukaniem wartosci najmniejszej (najwiekszej ) tej funkcji na A
Takie jest wzorcowe rozwiazanie na szostke .
7 mar 11:51
Saizou :
U mnie też taki wniosek można wyciągnąć, bo równość w nierówności między średnimi zachodzi
| | 1 | |
dla a=b, wówczas 2a=d ora 2b=d, czyli a=b= |
| d  |
| | 2 | |
W sumie nie doczytałem, że należy wskazać taki trójkąt, a nie wskazać minimalną wartość c.
7 mar 12:38
kerajs: 2) Wpisany jest okrąg o środku (0,−1) i promieniu 1.
Krzywa dla y<0 :
√(x−0)2+(y−(−1))2=−y+1
...
5)
| n(n−1) | | 2*n*3 | | 1 | | 3*2 | | 7 | |
| *1+ |
| * |
| + |
| *0< |
| |
| (n+3)(n+2) | | (n+3)(n+2) | | 2 | | (n+3)(n+2) | | 12 | |
3) zostaje dla tutejszych specjalistów−grafików
7 mar 17:07
Saizou :
Założenia:
log
x−y(x+y) ≤ 1
log
x−y(x+y) ≤ log
x−y(x−y)
| | x+y | |
a) 0<x−y<1 i |
| ≥ 1 (przypadek gdy logarytm jest malejący) |
| | x−y | |
| | x+y | |
b) x−y > 1 i 0 < |
| ≤ 1 (przypadek gdy logarytm jest rosnący) |
| | x−y | |
7 mar 18:12
Goblin:
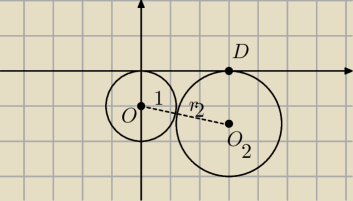
Dla y<0
probuje ustalic warunki
Punkt O=(0,−1)
Punkt O
2=(x,y) i y<0
|OO
2|=1+r
2
|DO
2|= r
2=
√(x−x)2+(−y−0)2=
√y2=y
dalej sie zawiesilem

7 mar 19:48
kerajs: Raczej:
|DO2|=....=|y|=−y=r2
|OO2|=1+r2
√x2+(y+1)2=1−y
7 mar 20:16
Goblin: Tak. Wlasnie teraz zauwazylem ze przeciez √y2=|y|
W naszym przypadku |y|=−y bo y<0
dzieki
7 mar 20:20
Goblin: To juz dokoncze
Dla y≥0 beda to okregi ktorych srodki leza na nieujemnej czeci osi OY
7 mar 20:28
kerajs: Tak.
7 mar 20:35
Goblin:
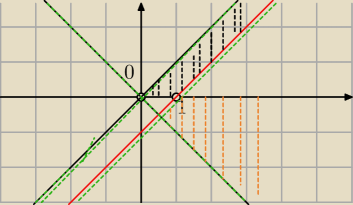
Zadanie nr 3
Wyszlo mi ogolnie tak
Proste o rownaniach sa y=x y=−x y=x−1
Same proste nie naleza do zbioru rozwiazan
Punkt (0,0) i (1,0) takze nie
Obszar zaznaczony na czarno gdy 0<x−y<1
Oszar zanaczony na pomaranczowo dla x−y>1
7 mar 20:38
 Do zadania pierwszego dodaję podpowiedź:
https://www.geogebra.org/geometry/yvykek2a
Do zadania pierwszego dodaję podpowiedź:
https://www.geogebra.org/geometry/yvykek2a
 Zad. 1
Zad. 1
 . Sa to zestawy na egzaminy wstepne na SGH (co sumie na jedno wychodzi )
. Sa to zestawy na egzaminy wstepne na SGH (co sumie na jedno wychodzi ) Dzięki Saizou .
Dzięki Saizou .
 Jakoś tak
Jakoś tak  może ktoś potwierdzi
może ktoś potwierdzi  δ = x
a+b = d
d2−2ab = a2+b2
Z nierówności między średnimi
Am ≥ Gm
δ = x
a+b = d
d2−2ab = a2+b2
Z nierówności między średnimi
Am ≥ Gm
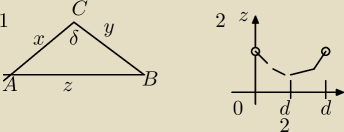 Saizou
To zadanie nr 4 gościu akuratnie pokazał jak rozwiazac wiec
AC=x BC=y x+y=d δ∊(0,π) AB=z
wielkosci d i δ sa dane
Stosujac do ΔABC tw cosinusow mamy
z2=x2+y2−2xycosδ
podstawiajac do tej rownosci y=d−x dostajemy
z2=x2+(d−x)2−2x(d−x)*cosδ
lub w postaci rownowaznej
z=√x2+(d−x)2−2x(d−x)cosδ=f(x)
W powyzszej rownosci x∊(0,d)
szukamy najmniejszej wartosci funkcji f(x) na zbiorze (0,d)
badamy w tym celu znak pochodnej funkcji f na przedziale (0,d)
Kolejno mamy
Saizou
To zadanie nr 4 gościu akuratnie pokazał jak rozwiazac wiec
AC=x BC=y x+y=d δ∊(0,π) AB=z
wielkosci d i δ sa dane
Stosujac do ΔABC tw cosinusow mamy
z2=x2+y2−2xycosδ
podstawiajac do tej rownosci y=d−x dostajemy
z2=x2+(d−x)2−2x(d−x)*cosδ
lub w postaci rownowaznej
z=√x2+(d−x)2−2x(d−x)cosδ=f(x)
W powyzszej rownosci x∊(0,d)
szukamy najmniejszej wartosci funkcji f(x) na zbiorze (0,d)
badamy w tym celu znak pochodnej funkcji f na przedziale (0,d)
Kolejno mamy

 Dla y<0
probuje ustalic warunki
Punkt O=(0,−1)
Punkt O2=(x,y) i y<0
|OO2|=1+r2
|DO2|= r2=√(x−x)2+(−y−0)2= √y2=y
dalej sie zawiesilem
Dla y<0
probuje ustalic warunki
Punkt O=(0,−1)
Punkt O2=(x,y) i y<0
|OO2|=1+r2
|DO2|= r2=√(x−x)2+(−y−0)2= √y2=y
dalej sie zawiesilem 
 Zadanie nr 3
Wyszlo mi ogolnie tak
Proste o rownaniach sa y=x y=−x y=x−1
Same proste nie naleza do zbioru rozwiazan
Punkt (0,0) i (1,0) takze nie
Obszar zaznaczony na czarno gdy 0<x−y<1
Oszar zanaczony na pomaranczowo dla x−y>1
Zadanie nr 3
Wyszlo mi ogolnie tak
Proste o rownaniach sa y=x y=−x y=x−1
Same proste nie naleza do zbioru rozwiazan
Punkt (0,0) i (1,0) takze nie
Obszar zaznaczony na czarno gdy 0<x−y<1
Oszar zanaczony na pomaranczowo dla x−y>1