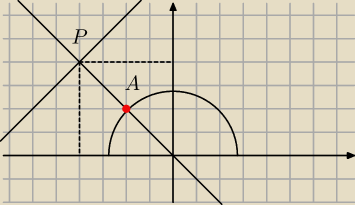
Okrag i rownanie Goblin: dany jest okrag x²+y²=8 i prosta y=x+8 Dla jakiego β∊R rownanie cos(a−x)=b−β ma rozwiazanie gdzie punkt S=(a,b) jest srodkiem okregu o najmniejszym promieniu stycznego do danego okregu i danej prostej Rownanie prostej prostopadlej do y=x+8 i przechodzacej przez punkt (0,0) to y=−x Punkty przeciecia prostej y=−x i okregu x²+y²=8 2x²=8 x²=4 x=−2 lub x=2 to y=2 lub y=−2 Biore do obliczen punkt A=(−2,2) Wspolrzedne punktu P=(−4,4) Srodek odcinka PA bedzie srodkiem szukanego okregu x_s=a=−3 y_s=b=3 rownanie ma postac cos(−3−x)=3−β ma wyjsc β∊<2,4>

kerajs: Skoro zbiorem wartości kosinusa (i sinusa ) jest przedział <−1,1> to równanie będzie miało rozwiązania gdy: −1≤3−β≤1 i stąd wynik.

Goblin: No tak . To oczywiste . Dziękuje Ci.