Planimetria
Kuba152: Znajdź zbiór wszystkich środków okręgów zewnętrznie stycznych do
okręgu o równaniu x2 + y2 = 4 i jednocześnie stycznych do prostej o równaniu y=−2.
6 mar 21:25
Kuba152: Dobra, już wyszło.
Robiłem błąd rachunkowy i nie wychodziło mi
6 mar 21:27
Goblin: To napisz rozwiazanie
6 mar 21:30
Kuba152:
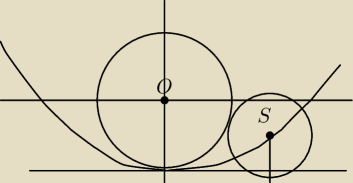
S=(a,b)
r=|b+2|
|OS| =
√a2+b2 = r+2
√a2+b2=|b+2| + 2
y=−2 więc
√a2+b2=b+4
a
2 + b
2 = b
2 + 8b + 16
8b= a
2 − 16
6 mar 21:46
Mila:
Ładne zadania rozwiązuje Kuba.
6 mar 21:52
Goblin: Kuba jednak nie okresliles czym jest ten zbior
6 mar 21:57
Kuba152: Hmm
No te punkty leżą na tej paraboli. Myślałem, że na tym można zakończyć.
Co w takim razie mam jeszcze zrobić?
6 mar 22:04
Goblin:
masz tak
wezmy np a=0 to wtedy b=−2
W tym punkcie nie dostaniesz rownania okregu bo r=0
wiec ten srodek nalezaloby wykluczyc
6 mar 22:21
Mila:
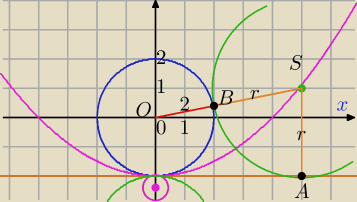
S=(x,y),
1) y ≥−2
|AS|=|BS|
|BS|=|OS|−2⇒|OS|=|BS|+2
|AS|=|y−(−2)|=|y+2|
(2+|y+2|)
2=x
2+y
2
4+4|y+2|+y
2+4y+4=x
2+y
2⇔
8+4|y+2|+4y=x
2, korzystając z założenia , że y≥−2 mamy |y+2|=y+2
8+4y+8+4y=x
2
| | 1 | |
środki okręgów leżą na paraboli y= |
| x2−2 dla y≥−2 |
| | 8 | |
2) natomiast dla y<−2
środki okręgów stycznych do danego okręgu i prostej y=−2 leżą na półprostej
x=0 i y<−2
6 mar 23:17
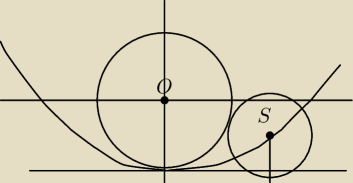 S=(a,b)
r=|b+2|
|OS| = √a2+b2 = r+2
√a2+b2=|b+2| + 2
y=−2 więc
√a2+b2=b+4
a2 + b2 = b2 + 8b + 16
8b= a2 − 16
S=(a,b)
r=|b+2|
|OS| = √a2+b2 = r+2
√a2+b2=|b+2| + 2
y=−2 więc
√a2+b2=b+4
a2 + b2 = b2 + 8b + 16
8b= a2 − 16
 S=(x,y),
1) y ≥−2
|AS|=|BS|
|BS|=|OS|−2⇒|OS|=|BS|+2
|AS|=|y−(−2)|=|y+2|
(2+|y+2|)2=x2+y2
4+4|y+2|+y2+4y+4=x2+y2⇔
8+4|y+2|+4y=x2, korzystając z założenia , że y≥−2 mamy |y+2|=y+2
8+4y+8+4y=x2
S=(x,y),
1) y ≥−2
|AS|=|BS|
|BS|=|OS|−2⇒|OS|=|BS|+2
|AS|=|y−(−2)|=|y+2|
(2+|y+2|)2=x2+y2
4+4|y+2|+y2+4y+4=x2+y2⇔
8+4|y+2|+4y=x2, korzystając z założenia , że y≥−2 mamy |y+2|=y+2
8+4y+8+4y=x2