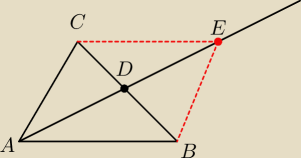
Dowód Goblin: W trójkącie ABC łączymy odcinkiem AD wierzchołek A ze środkiem D boku BC i na przedłużeniu odcinka AD odkłaadamy DE=AD Dowieść że AC=BE

Mila: Cechy przystawania Δ: bkb

Eta: Przekątne jakiego czworokąta dzielą się na połowy ? ..........

Goblin: Teraz pomyślałem tak Wykaże ze Δ ADC≡ΔEDB 1) AD=DE 2) DB=CD 3) ∡EDB=∡CDA jako wierzchołkowe Z cechy bkb Δ sa przystajace i z równosci tych wynika ze AC=BE

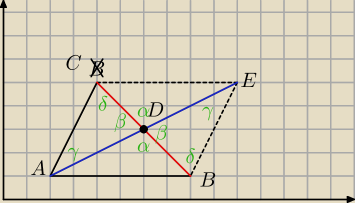
Saizou : ΔADC ≡ Δ EDB (bkb), zatem AC = BE

Goblin: Pomyslałem także o równoległoboku ale zadania jak juz pisalem zadania z klasy 8 i o figurach będzie pozniej

Goblin: Dziękuje za wszystkie uwagi .