Dla chętnych maturzystów ;)
Saizou :
Podrzucam zadanko z ukochanej przez
Etę geometrii.
Wyzwanie dla
Ety żeby znalazła najkrótsze rozwiązanie

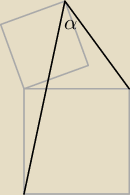
Na poniższym rysunku pole mniejszego kwadratu jest dwa razy mniejsze
od pola większego kwadratu.
Wyznacz miarę zaznaczonego kąta.
2 mar 20:42
60-latek:
Tu nie ma poniższego rysunku
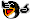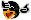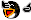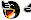
2 mar 21:09
2 mar 21:14
Saizou : Jak to nie, obróć monitor o 180 stopni

2 mar 21:24
Eta:

2 mar 21:25
Saizou : Maturzystów brak

2 mar 21:28
Eta:
Liczą,że matury nie będzie

2 mar 21:29
Saizou :
Oby nie, bo podobno w tym roku wg mnie będzie trudniej.
Wywalili tyle materiału, a zadań pewnie nie okroją tylko dadzą jakąś metodę
z wymagań egzaminacyjnych, która prowadzi przez Rio z Gdańska do Gdyni

2 mar 21:33
chichi:
Hej @
Saizou maturzystów nie brak, brak tylko tych ambitnych

2 mar 21:43
Goblin: Saizou ale kogo to tak bardzo obchodzi ?
Chyba tylko nauczycieli na ktorych rodzice zrzuca cała wine za zaistniala sytuacje a nie na
rzadzacych (to moje prywatne zdanie ) ktorzy zrobili wałek z pandemii
2 mar 21:45
Saizou :
To może ktoś inny się pokusi, aby rozwiązać zadanko

Politykę zostawmy, bo matematyka jest apolityczna

2 mar 21:50
Tles:
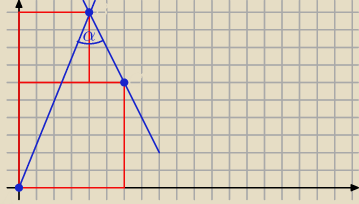
Można także w ten sposób przedstawić tę sytuację.
a
√2 − długość boku większego kwadratu, a − długość boku mniejszego kwadratu,
A=(0, 0), B=(a, a
√2+a), C=(a
√2, a
√2)
| | a√2+a−0 | |
prosta AB: y = a1x + b1, a1 = |
| =√2+1, |
| | a−0 | |
| | a√2+a−a√2 | | 1 | |
prosta BC: y = ax + b2, a2 = |
| = |
| =−1−√2 |
| | a−√2a | | 1−√2 | |
| | a1−a2 | | π | |
tgα = | |
| |=1, α= |
| |
| | 1+a1a2 | | 4 | |
2 mar 22:12
Saizou :
No można, ale dużo liczenia

.
Zresztą to zadanie można rozwiązać w podstawówce

Zadanie należy do działu geometria klasyczna.
2 mar 22:20
Tles:
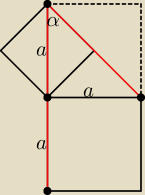
Albo tak, bez specjalnych obliczeń można określić, że α = 45 stopni
2 mar 22:34
circle:
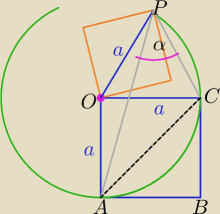
α− kąt wpisany w okrąg oparty na cięciwie AC
2 mar 23:03
Eta:
I o to, toto...

2 mar 23:08
chichi:
To ja też wrzucę coś prostego dla chętnych maturzystów albo forumowiczów

Niech cięciwa CD będzie prostopadła do średnicy AB, natomiast cięciwa AE dzieli promień OC na
pół, gdzie O jest środkiem okręgu. Wykaż, że cięciwa DE dzieli na pół cięciwę BC.
2 mar 23:18
Tles:
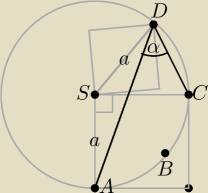
O łuk ABC oparty jest kąt środkowy ASC (kąt prosty) i kąt wpisany ADC
2 mar 23:19
Tles:
O już jest

, nie zauważyłem
2 mar 23:19
Eta:
Tles?

Ciekawe czy dostanę? jak zwykle.........
2 mar 23:34
Filip:
wrzuć jakieś zadanie z całek, a nie cały czas ta geometria na płaszczyźnie się przewija

Pzdr
Saizou 
2 mar 23:43
Saizou :

dla wszystkich rozwiązujących.
Filip e tam całki... geometria przyjemniejsza

3 mar 08:56
Saizou :
To może coś takiego.
Niech dana będzie funkcja f(x) = x2−3x+4.
Rozwiązać równanie f(f(f(x))) = x.
3 mar 09:07
piotr: f(x) = x spełnione tylko dla x=2
⇒
f(f(f(x))) = x spełnione tylko dla x=2
3 mar 12:55
Eta:
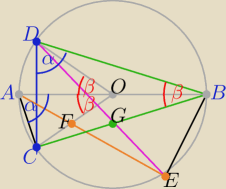
Zadanie od
chichi 2 marca 23:18
Dodać parę komentarzy...............
zatem ΔACO ∼ ΔCDB z cechy (kkk)
to AF jest środkową w ΔACO ( z treści zadania) to i DG jest środkową w ΔCDB
więc punkt G dzieli odcinek BC na połowy bo G ∊cięciwy DE
c.n.w.
3 mar 23:00
chichi:
Super @
Eta 
3 mar 23:09
tles:
Dla Ciebie
Eto 
3 mar 23:29
Eta:
Dziękuję
tles
Pozdrawiam

4 mar 14:33
 Podrzucam zadanko z ukochanej przez Etę geometrii.
Wyzwanie dla Ety żeby znalazła najkrótsze rozwiązanie
Podrzucam zadanko z ukochanej przez Etę geometrii.
Wyzwanie dla Ety żeby znalazła najkrótsze rozwiązanie  Na poniższym rysunku pole mniejszego kwadratu jest dwa razy mniejsze
od pola większego kwadratu.
Wyznacz miarę zaznaczonego kąta.
Na poniższym rysunku pole mniejszego kwadratu jest dwa razy mniejsze
od pola większego kwadratu.
Wyznacz miarę zaznaczonego kąta.
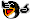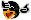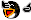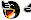






 Politykę zostawmy, bo matematyka jest apolityczna
Politykę zostawmy, bo matematyka jest apolityczna 
 Można także w ten sposób przedstawić tę sytuację.
a√2 − długość boku większego kwadratu, a − długość boku mniejszego kwadratu,
A=(0, 0), B=(a, a√2+a), C=(a√2, a√2)
Można także w ten sposób przedstawić tę sytuację.
a√2 − długość boku większego kwadratu, a − długość boku mniejszego kwadratu,
A=(0, 0), B=(a, a√2+a), C=(a√2, a√2)
 .
Zresztą to zadanie można rozwiązać w podstawówce
.
Zresztą to zadanie można rozwiązać w podstawówce  Zadanie należy do działu geometria klasyczna.
Zadanie należy do działu geometria klasyczna.
 Albo tak, bez specjalnych obliczeń można określić, że α = 45 stopni
Albo tak, bez specjalnych obliczeń można określić, że α = 45 stopni
 α− kąt wpisany w okrąg oparty na cięciwie AC
α− kąt wpisany w okrąg oparty na cięciwie AC

 Niech cięciwa CD będzie prostopadła do średnicy AB, natomiast cięciwa AE dzieli promień OC na
pół, gdzie O jest środkiem okręgu. Wykaż, że cięciwa DE dzieli na pół cięciwę BC.
Niech cięciwa CD będzie prostopadła do średnicy AB, natomiast cięciwa AE dzieli promień OC na
pół, gdzie O jest środkiem okręgu. Wykaż, że cięciwa DE dzieli na pół cięciwę BC.
 O łuk ABC oparty jest kąt środkowy ASC (kąt prosty) i kąt wpisany ADC
O łuk ABC oparty jest kąt środkowy ASC (kąt prosty) i kąt wpisany ADC
 , nie zauważyłem
, nie zauważyłem
 Ciekawe czy dostanę? jak zwykle.........
Ciekawe czy dostanę? jak zwykle.........
 Pzdr Saizou
Pzdr Saizou 
 dla wszystkich rozwiązujących.
Filip e tam całki... geometria przyjemniejsza
dla wszystkich rozwiązujących.
Filip e tam całki... geometria przyjemniejsza 
 Zadanie od chichi 2 marca 23:18
Dodać parę komentarzy...............
zatem ΔACO ∼ ΔCDB z cechy (kkk)
to AF jest środkową w ΔACO ( z treści zadania) to i DG jest środkową w ΔCDB
więc punkt G dzieli odcinek BC na połowy bo G ∊cięciwy DE
c.n.w.
Zadanie od chichi 2 marca 23:18
Dodać parę komentarzy...............
zatem ΔACO ∼ ΔCDB z cechy (kkk)
to AF jest środkową w ΔACO ( z treści zadania) to i DG jest środkową w ΔCDB
więc punkt G dzieli odcinek BC na połowy bo G ∊cięciwy DE
c.n.w.


