Oczywiste? - planimetria Tomasz: "Oblicz pole trapezu prostokątnego opisanego na okręgu, mając dane długości podstaw a i b" ... I teraz się pojawia pytanie − rozwiązania wskazują na to, żeby wyliczyć h i wstawić do wzoru. Rozwiązanie ma wyjść a * b Jednak czy nie można rozumować tak, że skoro trapez prostokątny jest opisany na okręgu to musi być prostokątem? (bo sumy przeciwległych beków muszą być takie same)

Tomasz: boków*

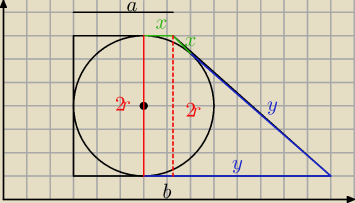
Saizou : x = a−r y = b−r x+y = a+b−2r Z tw. Pitagorasa (2r)² + (b−a)² = (a+b−2r)² 4r² + b²−2ab+b² = a²+b²+4r²+2ab−4ar−4br 4ab−4ar−4br=0 ab = r(a+b)

	ab
r =
	a+b

	1		ab
P=		(a+b)*2r = (a+b)*r = (a+b)*		= ab
	2		a+b

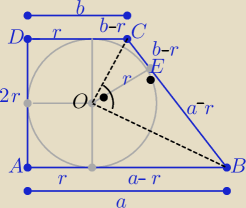
Eta: h=2r to P= (a+b)*r w ΔBOC r²=(a−r)(b−r) ⇒ ab=(a+b)*r= P P=ab ======