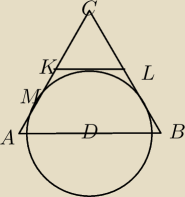 Dany jest trójkąt równoramienny ABC w którym AC=BC=6 a punkt D jest środkiem podstawy AB. Okrąg
o środku D jest styczny do prostej AC w punkcie M. Punkt K leży na boku AC, punkt L leży na
boku BC, odcinek KL jest styczny do rozważanego okręgu oraz KC=LC=2.
Dany jest trójkąt równoramienny ABC w którym AC=BC=6 a punkt D jest środkiem podstawy AB. Okrąg
o środku D jest styczny do prostej AC w punkcie M. Punkt K leży na boku AC, punkt L leży na
boku BC, odcinek KL jest styczny do rozważanego okręgu oraz KC=LC=2.
| AM | 4 | |||
Wykaż że | = | |||
| MC | 5 |
| 1 | ||
Wyszły mi trójkąty podobne CPK i CDA k= | i PD=MD=2x | |
| 3 |
| PK | MD | 4 | ||||
Kolejne trójkąty podobne to CPK i CMD stąd | = | stąd PK= | ||||
| CK | CD | 3 |
| 8 | ||
W rozwiązaniu było napisane, że AM= | ale kompletnie nie wiem skąd to się wzięło. | |
| 3 |
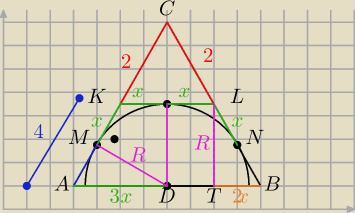 AM = 4−x
AD = 3x
Z Pitagorasa MD
R2 + (4−x)2 = (3x)2
R2 = (3x)2−(4−x)2
Z Pitagorasa w LTB
R2 + (2x)2 = 42
(3x)2−(4−x)2 + (2x)2 = 16
9x2−16+8x−x2+4x2 = 16
12x2+8x = 0
AM = 4−x
AD = 3x
Z Pitagorasa MD
R2 + (4−x)2 = (3x)2
R2 = (3x)2−(4−x)2
Z Pitagorasa w LTB
R2 + (2x)2 = 42
(3x)2−(4−x)2 + (2x)2 = 16
9x2−16+8x−x2+4x2 = 16
12x2+8x = 0
| 8 | 2 | |||
x = | = | |||
| 12 | 3 |
| 2 | 10 | |||
AM = 4 − | = | |||
| 3 | 3 |
| 10 | 8 | |||
MC = 6 − | = | |||
| 3 | 3 |
| MC | 10 | 3 | 5 | ||||
= | * | = | |||||
| AM | 3 | 8 | 4 |
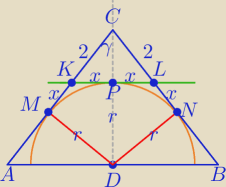 |AK|=|BL|=4
|AK|=|BL|=4

| 8 | ||
Chodzi mi tylko o ten jeden moment kiedy AM= | . tylko tego nie rozumiem skąd się wzięło | |
| 3 |
| 2 | 1 | |||
ΔCPK∼ΔCDA w skali k= | = | ⇒ | ||
| 6 | 3 |
| x | AM | |||
sinγ= | w ΔCPK i sinD= | |||
| 2 | AD |
| x | 4−x | ||
= | |||
| 2 | 3x |
| 4 | ||
x=−2∉D lub x= | ( tak jak obliczyłaś !) | |
| 3 |
| 4 | 8 | |||
|AM|=4− | = | |||
| 3 | 3 |
| 4 | 10 | |||
|MC|=2+ | = | |||
| 3 | 3 |
| AM | 8 | 3 | 4 | ||||
= | * | = | |||||
| MC | 3 | 10 | 5 |
 dzięki wielkie
za pomoc
dzięki wielkie
za pomoc
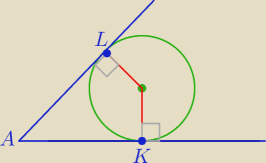 Tak myślałam, że nie zauważyłaś,
że punkty styczności okręgu są jednakowo odległe od wierzchołka kąta.
|AK|=|AL|
Tak myślałam, że nie zauważyłaś,
że punkty styczności okręgu są jednakowo odległe od wierzchołka kąta.
|AK|=|AL|
 Jak masz jeszcze chwilkę to nakierujesz mnie co dalej?
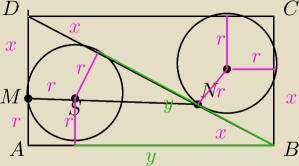
Dany jest prostokąt ABCD. Okrąg wpisany w trójkąt BCD jest styczny do przekątnej BD w punkcie
N. Okrąg wpisany w trójkąt ABD jest styczny do boku AD w punkcie M, a środek S tego okręgu
leży na odcinku MN. Wykaż że |MN|=|AD|
Zaczęłam tak jak narysowałam kolorkiem. Ale co teraz?
Jak masz jeszcze chwilkę to nakierujesz mnie co dalej?
Dany jest prostokąt ABCD. Okrąg wpisany w trójkąt BCD jest styczny do przekątnej BD w punkcie
N. Okrąg wpisany w trójkąt ABD jest styczny do boku AD w punkcie M, a środek S tego okręgu
leży na odcinku MN. Wykaż że |MN|=|AD|
Zaczęłam tak jak narysowałam kolorkiem. Ale co teraz?

