statystyka js: gestosc zmiennej losowej X dana jest wzorem f(x) = { (2/9)*x dla x∊(0,3) } { 0 dla pozostalych } musze to teraz zamienic na dystrybuante, jak to zrobic

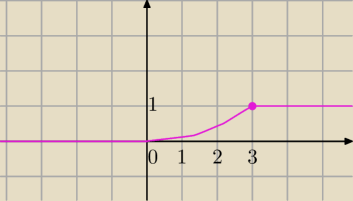
ICSP:

	⎧	0 dla x ≤ 0
F(x) = ∫−∞x f(x) dx =	⎨	x2/9 dla x ∊(0;3)
	⎩	1 dla x ≥ 3

Mila: Przedziały: { (−∞,0>, (0,3>, (3,∞)} 1) F(x)=_−∞∫⁰0dt=0 dla x<0 ====================

	2
2) F(x)=−∞∫00dt+0∫x(		t)dt+3∫∞0dt=
	9

	2		1
F (x)=[		*		t2]0x=
	9		2

	1
F(x)=		x2 dla 0<x≤3
	9

==================

	2		1		1
3) F(x)=−∞∫∞(		t dt)=[		t2]03=		*9=1 dla t>3
	9		9		9

F(x)=1 dla x>3 ===============

js: czemu w ostatnim kroku liczymy calke oznaczona od 0 do 3 po tym co wyszlo w 2 punkcie?

Mila: Dystrybuanta przedstawia kumulowane szanse . Wyznaczamy z funkcji gęstości w każdym następnym przedziale uwzględniając poprzednie przedziały. 3) x>3 Zatem :

	2		1
F(x)=−∞∫0dt+0∫3		t dt+3∫∞0dt=0+[		t2]03 +0=1
	9		9

Mila: Poprawiam początek zapisu: F(x)=_−∞∫⁰ 0dt+..

js: a jak mam dystrybuante F(x) = { 0 dla x <= 0 } { (x/67)⁴ dla x ∊ (0, 67> } { 1 dla x > 67 } i chce obliczyc gestosc, to po prostu licze pochodna z kazdego przedzialu? (0)' = 0 ((x/67)⁴)' = (4x/67)³ (1)' = 0 czyli gestosc f(x) = { (4x/67)³ dla x ∊ (0,67> } { 0 dla x nie nalezacego do (0, 67> } tak?

Mila: Tak liczysz pochodną w przedziałach. dystrybuanta : 1) F(x)=(x/67)⁴ dla x ∊ (0, 67> 2) Funkcja gęstości:

	1		4x3
f(x)=(		*x4)'=
	674		674

	4x3
f(x)=		dla x∊(0,67>
	674

f(x) = 0 dla x≤0 f(x)=0 dla x>67 Teraz sprawdzasz czy _−∞∫^∞f(t) dt=1

js: a jak calka nie wyjdzie 1 to co?

Mila: To sprawdzasz, czy dobrze obliczyłeś pochodną. Może też być błędny wzór dystrybuanty.